Tabla de Contenidos
Segundo Parcial - Análisis Matemático I - 2005
Cátedra: Sede Drago
Fecha: 2º Cuatrimestre 2005
Enunciado
Punto I
Sea 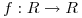 tal que
tal que 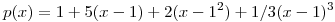 es el polinomio de Taylor de F de orden 3 en
es el polinomio de Taylor de F de orden 3 en  y
y 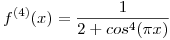 ,
,  . Hallar el polinomio de Taylor de
. Hallar el polinomio de Taylor de 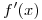 de orden 2 en
de orden 2 en  y estimar el error que se comete al calcular
y estimar el error que se comete al calcular 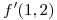 por medio del polinomio hallado.
por medio del polinomio hallado.
Punto II
Hallar una función f con derivada continua que satisfaga 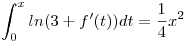 ,
, 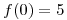 .
.
Punto III
Calcular el área de la región comprendida entre el gráfico de 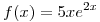 y el eje x para
y el eje x para 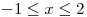 .
.
Punto IV
Encontrar todos los valores de  para los cuales la serie
para los cuales la serie 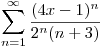 sea convergente. Indique para qué valores la convergencia es condicional.
sea convergente. Indique para qué valores la convergencia es condicional.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
