Tabla de Contenidos
Parcial - CBC - 28. Análisis Matemático I - 2010
Fecha: 30/06/10
Parcial: 2º Parcial - 1º cuatrimestre 2010
Enunciado
Punto I
Sea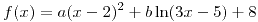 
. Hallar los valores de 
y 
en 
para que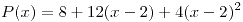 
sea el polinomio de Taylor de orden 
en 
de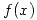 
.
Punto II
Hallar una función derivable en 
que satisfaga 
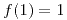y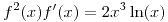 
.
Punto III
Calcular el área encerrada entre los gráficos de las funciones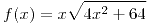 
y 
.
Punto IV
Hallar todos los valores de 
tales que la serie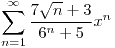 
sea convergente.
Resolución
Si alguno tiene ganas de resolverlo, no dude en editar.
Punto I
Punto II
Punto III
Punto IV
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
