Segundo Parcial - Análisis Matemático I - 2008
Cátedra: Sede Drago
Fecha: 1º Cuatrimestre 2008
Enunciado
Punto I
Sea 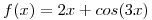 . Hallar el polinomio de Taylor
. Hallar el polinomio de Taylor 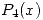 de orden 4 de
de orden 4 de 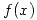 en
en  . Mediante la fórmula del resto, estimar el error que se comete al aproximar
. Mediante la fórmula del resto, estimar el error que se comete al aproximar 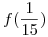 por
por 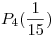 .
.
Punto II
Hallar una función 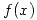 continua y derivable tal que
continua y derivable tal que  y
y  .
.
Punto III
Calcular el área de la región comprendida entre el grafico de ![<tex>f(x) = (x-3)\sqrt[3]{6x-x^2}</tex> <tex>f(x) = (x-3)\sqrt[3]{6x-x^2}</tex>](lib/plugins/latex/images/962db1a19b8999cab1e76f8f992145f2df054d0d_0.png) y el de
y el de 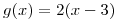 .
.
Punto IV
Hallar todos los 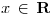 tales que la serie
tales que la serie 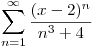 converge.
converge.
Resolución
Punto I
Nos piden hallar el polinomio de Taylor de orden 4 de 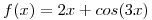 , bueno empecemos a derivar la funcion
, bueno empecemos a derivar la funcion 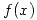 hasta su cuarta derivada
hasta su cuarta derivada
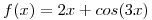 entonces
entonces 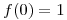
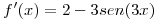 entonces
entonces 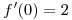
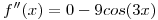 entonces
entonces 
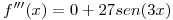 entonces
entonces 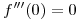
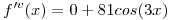 entonces
entonces 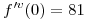
Armemos el Polinomio de Taylor:
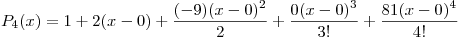
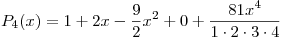
Entonces el Polinomio de Taylor pedido es: 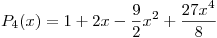
Ahora pasamos a calcular el error cometido al aproximar 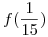 por
por 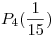
Veamos la formula del resto:
Formula del resto:
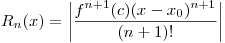 con
con  entre
entre 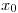 y
y 
Aplicado al Ejemplo: 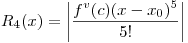 con
con  entre
entre 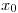 y
y 
ahora pasemos a calcular 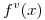
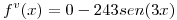
Ahora se calcula la formula del resto con  :
:
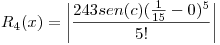 con
con  entre
entre 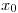 y
y 
Se acota el resto, como se tiene 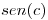 que es una funcion oscilante (entre -1 y 1) en módulo, entonces el valor máximo que puede tomar
que es una funcion oscilante (entre -1 y 1) en módulo, entonces el valor máximo que puede tomar 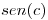 es
es 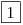 , asi que para acotar el resto considero a
, asi que para acotar el resto considero a  .
.
Entonces nos queda:
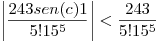
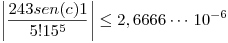
Entonces el error que se comete al calcular 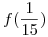 por
por 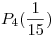 es
es 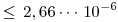 .
.
Punto II
Este es un ejercicio típico de Ecuaciones Diferenciales, tenemos la siguiente ecuación diferencial:

despejemos un poco:
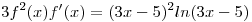
ahora pasemos a integrar ambas partes:
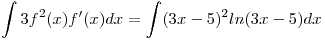
Ahora integramos cada parte por separado, empecemos por:
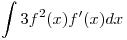 entonces aplico el metodo de sustitución
entonces aplico el metodo de sustitución 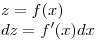 ahora reemplazo en la integral:
ahora reemplazo en la integral:
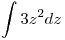 opero:
opero: 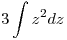 entonces
entonces 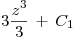 , por lo tanto la primitiva de
, por lo tanto la primitiva de 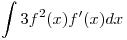 es
es 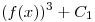
Seguimos con:
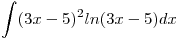 , aca se va a utilizar el Metodo de Integracion por partes:
, aca se va a utilizar el Metodo de Integracion por partes: 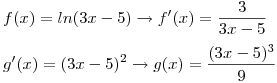 entonces nos queda:
entonces nos queda:
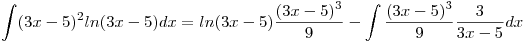 entonces nos queda:
entonces nos queda:
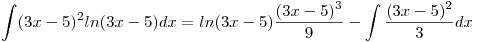
Ahora nos queda solo integrar: 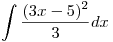 , Operamos…
, Operamos…
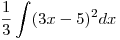 entonces nos queda
entonces nos queda 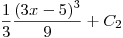
Por lo tanto la primitiva de:
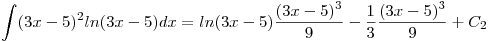 simplificamos un poco:
simplificamos un poco:
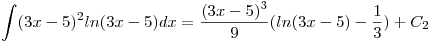
y ahora reemplazamos en la igualdad de arriba:
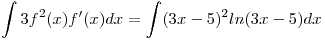 ahora nos queda como…
ahora nos queda como…
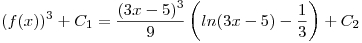
juntamos las constantes y pasamos la potencia como raiz y nos queda:
![<tex>f(x)= \sqrt[3]{\frac{(3x-5)^3}{9} \left( ln(3x-5) - \frac{1}{3} \right) + C} </tex> <tex>f(x)= \sqrt[3]{\frac{(3x-5)^3}{9} \left( ln(3x-5) - \frac{1}{3} \right) + C} </tex>](lib/plugins/latex/images/159f15f80e92ee5b8c9c3011e48d90a3bee71185_0.png) donde
donde 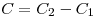 .
.
Ahora para terminar de sacar 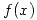 se tiene q calcular el valor de
se tiene q calcular el valor de  y para eso se usa el dato que nos dan que es
y para eso se usa el dato que nos dan que es 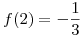 entonces:
entonces:
![<tex>f(2)= \sqrt[3]{\frac{(1)^3}{9} \left( ln(1) - \frac{1}{3} \right) + C}</tex> <tex>f(2)= \sqrt[3]{\frac{(1)^3}{9} \left( ln(1) - \frac{1}{3} \right) + C}</tex>](lib/plugins/latex/images/114852ce9dcc1ad0cd519582962192d750b3ebaf_0.png)
![<tex> -\frac{1}{3}= \sqrt[3]{\frac{1}{9} \left( -\frac{1}{3} \right) + C}</tex> <tex> -\frac{1}{3}= \sqrt[3]{\frac{1}{9} \left( -\frac{1}{3} \right) + C}</tex>](lib/plugins/latex/images/3ea64ab0094816f551b631684bddfcbecfe9c48f_0.png)
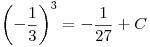
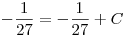
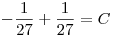
entonces nos queda q 
por lo tanto la funcion 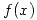 pedida es:
pedida es:
![<tex>f(x)= \sqrt[3]{\frac{(3x-5)^3}{9} \left( ln(3x-5) - \frac{1}{3} \right)} </tex> <tex>f(x)= \sqrt[3]{\frac{(3x-5)^3}{9} \left( ln(3x-5) - \frac{1}{3} \right)} </tex>](lib/plugins/latex/images/7e2c9079ac93294016b9455c3ae9fdabe628b8da_0.png)
Punto III
Este ejercicio consiste en calcular el area entre 2 curvas, para eso se tiene que utilizar las tan conocidas integrales.
Tenemos la curva ![<tex>f(x) = (x-3)\sqrt[3]{6x-x^2}</tex> <tex>f(x) = (x-3)\sqrt[3]{6x-x^2}</tex>](lib/plugins/latex/images/962db1a19b8999cab1e76f8f992145f2df054d0d_0.png) y la curva
y la curva 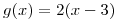 , para hallar el area entre esas 2 curvas, tenemos que primero buscar, en que puntos se interseccionan (o vulgarmente dicho, se cruzan), pasemos a buscarlos:
, para hallar el area entre esas 2 curvas, tenemos que primero buscar, en que puntos se interseccionan (o vulgarmente dicho, se cruzan), pasemos a buscarlos:
![<tex>(x-3)\sqrt[3]{6x-x^2} \,= \, 2(x-3)</tex> <tex>(x-3)\sqrt[3]{6x-x^2} \,= \, 2(x-3)</tex>](lib/plugins/latex/images/1361378ca16d861b9dd998952017ef9714569d71_0.png) , uno de los puntos de intersección se ve a simple vista y es
, uno de los puntos de intersección se ve a simple vista y es  , ahora pasemos a buscar el/los otro/s punto/s:
, ahora pasemos a buscar el/los otro/s punto/s:
![<tex>(x-3)\sqrt[3]{6x-x^2} \,= \, 2(x-3)</tex> <tex>(x-3)\sqrt[3]{6x-x^2} \,= \, 2(x-3)</tex>](lib/plugins/latex/images/1361378ca16d861b9dd998952017ef9714569d71_0.png) opero:
opero:
![<tex>\sqrt[3]{6x-x^2} \,= \, 2</tex> <tex>\sqrt[3]{6x-x^2} \,= \, 2</tex>](lib/plugins/latex/images/c0659eaaef1b5dad78276354b96db9101c1bc80e_0.png)
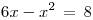
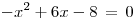 y de esta ecuacion cuadrática sale q los otros 2 puntos de intersección son:
y de esta ecuacion cuadrática sale q los otros 2 puntos de intersección son:  y
y 
En resumen los puntos de interseccion entre las curvas 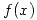 y
y  son
son 
ahora vamos a averiguar cual es el “techo” y cual es el “piso” entre los intervalos formados por los puntos hallados:
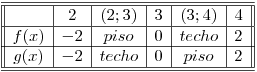
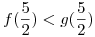
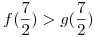
Ahora pasamos a armar las integrales, para que recuerden como era el area entre curvas, a continuación voy a poner un caso general:
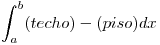 , ahora pasamos a armar las integrales:
, ahora pasamos a armar las integrales:
![<tex>\int_2^3 2(x-3) - (x-3)\sqrt[3]{6x-x^2}dx \, + \, \int_3^4 (x-3)\sqrt[3]{6x-x^2} - 2(x-3)dx</tex> <tex>\int_2^3 2(x-3) - (x-3)\sqrt[3]{6x-x^2}dx \, + \, \int_3^4 (x-3)\sqrt[3]{6x-x^2} - 2(x-3)dx</tex>](lib/plugins/latex/images/8201ed37ef65378d29f8eafa8b37b6e43fdce6f2_0.png) , lo unico q nos queda es calcular las integrales por separado, empezemos con:
, lo unico q nos queda es calcular las integrales por separado, empezemos con:
![<tex>\int_2^3 2(x-3) - (x-3)\sqrt[3]{6x-x^2}dx</tex> <tex>\int_2^3 2(x-3) - (x-3)\sqrt[3]{6x-x^2}dx</tex>](lib/plugins/latex/images/b6adacf695b3c94cfef67f417d2bea70874cf691_0.png) , opero:
, opero:
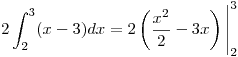 por lo tanto:
por lo tanto:

Ahora paso a calcular:
![<tex>\int_2^3 (x-3)\sqrt[3]{6x-x^2}dx</tex> <tex>\int_2^3 (x-3)\sqrt[3]{6x-x^2}dx</tex>](lib/plugins/latex/images/6b0d50c9d5cc5d544df577744f5cda627aafa22c_0.png) aplico el metodo de sustitucion:
aplico el metodo de sustitucion: 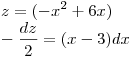 reemplazo en la integral y CAMBIO LOS LIMITES DE INTEGRACION!:
reemplazo en la integral y CAMBIO LOS LIMITES DE INTEGRACION!:
![<tex> -\frac{1}{2} \int_8^9 \sqrt[3]{z}dz</tex> <tex> -\frac{1}{2} \int_8^9 \sqrt[3]{z}dz</tex>](lib/plugins/latex/images/07320e9682d938696cadd514b23afb2018d465e4_0.png) , opero:
, opero: ![<tex> -\frac{1}{2} \left( \frac{3}{4}z^{\frac{4}{3}} \right) \Bigg|_8^9 \, = \, -\frac{3}{8} (\sqrt[3]{6561}-16)</tex> <tex> -\frac{1}{2} \left( \frac{3}{4}z^{\frac{4}{3}} \right) \Bigg|_8^9 \, = \, -\frac{3}{8} (\sqrt[3]{6561}-16)</tex>](lib/plugins/latex/images/a31f3cfed2710fd6182c72484c480ccfdc1f98b0_0.png) .
.
Por lo tanto la:
![<tex>\int_2^3 2(x-3) - (x-3)\sqrt[3]{6x-x^2}dx \, = \, -1 \, + \, \frac{3}{8} (\sqrt[3]{6561}-16) </tex> <tex>\int_2^3 2(x-3) - (x-3)\sqrt[3]{6x-x^2}dx \, = \, -1 \, + \, \frac{3}{8} (\sqrt[3]{6561}-16) </tex>](lib/plugins/latex/images/a1606861da136c1fd2bd83a5a860ceca591a02a8_0.png)
Ahora pasemos a calcular(como en parte ya se calculo, me limito a mostrarles el resultado, con el procedimiento, pueden verificarlos uds):
![<tex>\int_3^4 (x-3)\sqrt[3]{6x-x^2} - 2(x-3)dx \, = \, -\frac{1}{2} \left( \frac{3}{4}z^{\frac{4}{3}} \right) \Bigg|_9^8 \, - \, 2 \left( \frac{(x-3)^2}{2} \right) \Bigg|_3^4 \, = \\ = \, -\frac{3}{8} (16 - \sqrt[3]{6561}) - 1</tex> <tex>\int_3^4 (x-3)\sqrt[3]{6x-x^2} - 2(x-3)dx \, = \, -\frac{1}{2} \left( \frac{3}{4}z^{\frac{4}{3}} \right) \Bigg|_9^8 \, - \, 2 \left( \frac{(x-3)^2}{2} \right) \Bigg|_3^4 \, = \\ = \, -\frac{3}{8} (16 - \sqrt[3]{6561}) - 1</tex>](lib/plugins/latex/images/43bbe82d6798368ea528d2c0574bc590895ac970_0.png)
y por ultimo solo resta sumar ambos resultados:
![<tex> (-1 \, + \, \frac{3}{8} (\sqrt[3]{6561}-16)) \, + \, (-\frac{3}{8} (16 - \sqrt[3]{6561}) - 1) \, = \, \frac{3}{4} \sqrt[3]{6561} - 12 </tex> <tex> (-1 \, + \, \frac{3}{8} (\sqrt[3]{6561}-16)) \, + \, (-\frac{3}{8} (16 - \sqrt[3]{6561}) - 1) \, = \, \frac{3}{4} \sqrt[3]{6561} - 12 </tex>](lib/plugins/latex/images/ab4374ebaff90a42ee8162177ae55d5ce46b3631_0.png)
Por lo tanto el Área entre la región comprendida entre las curvas ![<tex>f(x) = (x-3)\sqrt[3]{6x-x^2}</tex> <tex>f(x) = (x-3)\sqrt[3]{6x-x^2}</tex>](lib/plugins/latex/images/962db1a19b8999cab1e76f8f992145f2df054d0d_0.png) y
y 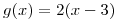 es:
es:
![<tex> \frac{3}{4} \sqrt[3]{6561} - 12 </tex> <tex> \frac{3}{4} \sqrt[3]{6561} - 12 </tex>](lib/plugins/latex/images/645ee2519262b4823e9fdc2d4a1f737ca0ea8fe5_0.png)
Punto IV
Tenemos la siguiente serie: 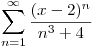 , primero tenemos que ver que tipo de Serie es:
, primero tenemos que ver que tipo de Serie es:
Como se ve a simple vista, esta Serie, se trata de una Serie de Potencia, ahora pasamos a buscar todos 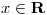 , para eso se tiene que estudiar el módulo de la Seria dada:
, para eso se tiene que estudiar el módulo de la Seria dada:
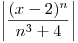 , entonces nos queda
, entonces nos queda 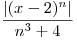 , Ahora apliquemos el Criterio de Cauchy
, Ahora apliquemos el Criterio de Cauchy
forma genérica: ![<tex> \lim_{n \to \infty} \sqrt[n]{a_n}</tex> <tex> \lim_{n \to \infty} \sqrt[n]{a_n}</tex>](lib/plugins/latex/images/c265c9a02b8b13fdec9a763a9a99c47c6cebe0bb_0.png) , ahora apliquemos a la serie:
, ahora apliquemos a la serie:
![<tex> \lim_{n \to \infty} \sqrt[n]{\frac{|(x-2)^n|}{n^3+4}} </tex> <tex> \lim_{n \to \infty} \sqrt[n]{\frac{|(x-2)^n|}{n^3+4}} </tex>](lib/plugins/latex/images/ade3a49d7425b47c781087229893fbdc05360bf1_0.png) , distribuyo:
, distribuyo: ![<tex>\lim_{n \to \infty}\frac{\sqrt[n]{|(x-2)^n|}}{\sqrt[n]{n^3+4}}</tex> <tex>\lim_{n \to \infty}\frac{\sqrt[n]{|(x-2)^n|}}{\sqrt[n]{n^3+4}}</tex>](lib/plugins/latex/images/9bd9ca02ec90e16b9356c1016024a44779dd8227_0.png) , ahora calculo cada límite por separado:
, ahora calculo cada límite por separado:
![<tex> \lim_{n \to \infty} \sqrt[n]{n^3+4} \, = \, \lim_{n \to \infty} \sqrt[n]{n^3}\sqrt[n]{1+\frac{4}{n^3}} \,= \, 1 </tex> <tex> \lim_{n \to \infty} \sqrt[n]{n^3+4} \, = \, \lim_{n \to \infty} \sqrt[n]{n^3}\sqrt[n]{1+\frac{4}{n^3}} \,= \, 1 </tex>](lib/plugins/latex/images/9ecee01944885e15ceb64a3a57a36136f56421ff_0.png)
ahora me queda:
 , ahora para que nuestra Serie converja, el
, ahora para que nuestra Serie converja, el 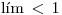 , entonces:
, entonces:
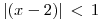 , desarrollo el módulo y nos queda:
, desarrollo el módulo y nos queda: 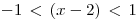 , opero:
, opero:
 , entonces la serie converge para todo
, entonces la serie converge para todo 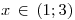
El intervalo hallado no es el correcto, ya que uno suponte que la serie converge dentro del intervalo pero no en los bordes, para eso lo unico que resta hacer es analizar los bordes:
Para  :
:
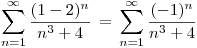 , es una Serie aleternada.
, es una Serie aleternada.
Apliquemos el Criterio de Liebnitz:
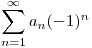 , donde
, donde 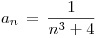
veamos si satisface las 3 hipotesis del criterio de Liebnitz:
1)  es positiva? : Si porque es una suma de positivos
es positiva? : Si porque es una suma de positivos 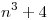 para todo
para todo 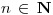
2)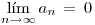 ? : si ya que
? : si ya que 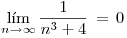
3)  es decreciente? : para que
es decreciente? : para que  sea decreciente, tiene que satisfacer la siguiente desigualdad
sea decreciente, tiene que satisfacer la siguiente desigualdad 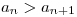 , veamos si es cierto esto:
, veamos si es cierto esto:
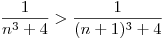 , opero:
, opero: 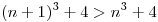 , por lo tanto, satisface la igualdad
, por lo tanto, satisface la igualdad 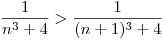 , entonces
, entonces  es decreciente.
es decreciente.
Cumplidas las 3 hipotesis del Criterio de Liebnitz, podemos asegurar que la Serie converge Absolutamente cuando 
Para  :
:
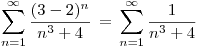 , utilizamos el criterio de comparacion con
, utilizamos el criterio de comparacion con 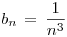 :
:
como  , y como
, y como  es una Serie P con P > 1, entonces Converge.
es una Serie P con P > 1, entonces Converge.
Por lo tanto 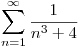 también converge cuando
también converge cuando  .
.
Por lo tanto la Serie 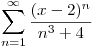 converge para todo
converge para todo ![<tex>x \, \in \, [1;3]</tex> <tex>x \, \in \, [1;3]</tex>](lib/plugins/latex/images/2808f2edbd15de8bdff9719b7c99db4bbfca56d6_0.png)
