Primer Parcial - Análisis Matemático I - 2005
- Enunciado
  - Punto I
  - Punto II
  - Punto III
  - Punto IV

Primer Parcial - Análisis Matemático I - 2005

Cátedra: Sede Drago
Fecha: 2º Cuatrimestre 2005

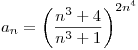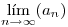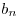Sea $<tex>a_n= \left (\frac {n^3+4}{n^3+1} \right )^{2n^4}</tex>$ . Calcular el $<tex>\lim_{n \to \infty} (a_n)</tex>$ y si $<tex>b_n</tex>$ es una sucesión que tiene límite, finito o infinito, y tal que 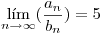$<tex>\lim_{n \to \infty} (\frac {a_n}{b_n})=5</tex>$ , determinar $<tex>\lim_{n \to \infty} (b_n)</tex>$ .

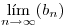Punto II

Sea 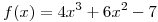$<tex>f(x)=4x^3+6x^2-7</tex>$ . Determinar un punto del gráfico de F donde la recta tangente en ese punto sea paralela a la recta tangente en el punto 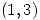$<tex>(1,3)</tex>$ . Hallar la ecuación de dicha recta.

Punto III

Hallar todos los valores de 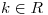$<tex>k \in R</tex>$ para los cuales la ecuación 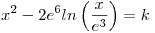$<tex>x^2-2e^6 ln \left ( \frac {x}{e^3} \right ) =k</tex>$ tiene dos soluciones.

Punto IV

Dada 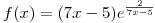$<tex>f(x)=(7x-5)e^{ \frac {2}{7x-5}}</tex>$ , hallar dominio, intervalos de crecimiento y decrecimiento, máximos, mínimos relativos y asíntotas de F. Con la información obtenida hacer un gráfico de F.

Primer Parcial - Análisis Matemático I - 2005

Enunciado

Punto I

Punto II

Punto III

Punto IV