Tabla de Contenidos
Parcial - CBC - 28. Análisis Matemático I - 2009
Parcial: 1º Parcial - 1º cuatrimestre 2009
Enunciado
Punto I
Hallar  y
y 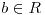 , para que
, para que 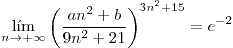 .
.
Punto II
Sea ![<tex>f:\ [-2,0] \rightarrow R</tex> <tex>f:\ [-2,0] \rightarrow R</tex>](lib/plugins/latex/images/633f8111fa6f204af88cbb139b021ef2fe6d57be_0.png) ,
,
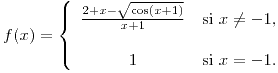
Mediante el estudio del cociente incremental, calcular, si existe, 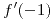 .
.
Punto III
Hallar todos los valores de 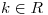 para los cuales la ecuación
para los cuales la ecuación 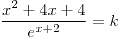 tiene solución única.
tiene solución única.
Punto IV
Hallar dos números reales positivos  e
e  , menores de 1, tales que su suma sea igual a
, menores de 1, tales que su suma sea igual a  y tales que
y tales que 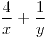 sea mínimo.
sea mínimo.
Resolución
Si alguno tiene ganas de resolverlo, no dude en editar.
Punto I
Punto II
Punto III
Punto IV
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
