Examen Parcial - cbc.28. Análisis Matemático I - 1° Cuatrimestre 2006
Fecha: 1° Cuatrimestre 2006
Tema: 2
Enunciado
Punto I
Sea  una sucesión de términos positivos definida como
una sucesión de términos positivos definida como
![<tex> $ \begin{equation}\nonumber a_1=1, \quad a_{n+1}=\frac{\sqrt[n]{n+3}}{2}a_n, \qquad n \in \mathbf{N} \end{equation} $ </tex> <tex> $ \begin{equation}\nonumber a_1=1, \quad a_{n+1}=\frac{\sqrt[n]{n+3}}{2}a_n, \qquad n \in \mathbf{N} \end{equation} $ </tex>](lib/plugins/latex/images/ea0f747d23784e2dc518f869c53ec443eaa9fad4_0.png)
Calcular, si existe, el  .
.
Punto II
La recta tangente al gráfico de  en
en  es
es  . Determinar los valores de
. Determinar los valores de  y
y  y hallar la ecuación de la recta tangente al gráfico de
y hallar la ecuación de la recta tangente al gráfico de  en
en  .
.
Punto III
Hallar la cantidad de soluciones de la ecuación  , siendo
, siendo
 .
.
Punto IV
Hallar la distancia mínima del punto  a la parábola
a la parábola  .
.
Resolución
Punto IV
Es un problema de Optimización donde se minimizará el cuadrado de la Distancia ( ).
).
La ecuación de la distancia es la siguiente:

Luego, reemplazando los datos:  ;
;  ;
;  desarrollando, queda así:
desarrollando, queda así:
 Luego,
Luego,

y ordenando, queda: 
Por comodidad, escribimos que 
Derivamos  e igualamos a cero para obtener los puntos críticos:
e igualamos a cero para obtener los puntos críticos:


![<tex>x = \sqrt[3]{\frac{1}{{64}}}</tex> <tex>x = \sqrt[3]{\frac{1}{{64}}}</tex>](lib/plugins/latex/images/219b720eb720b66e3f6e70f802fb0ac4f13dd213_0.png)

Para verificar si es un máximo o un mínimo, lo hacemos con la segunda derivada:
Si  , entonces
, entonces  es un MÍNIMO
es un MÍNIMO
Si  , entonces
, entonces  es un MÁXIMO
es un MÁXIMO
Entonces, siguiendo este criterio, nos queda:

Reemplazando  en
en 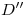 tenemos:
tenemos:

De esta manera, decimos que  es un MÍNIMO.
es un MÍNIMO.
Ahora, reemplazando  en
en 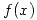 obtenemos
obtenemos  :
:

Por lo tanto, la distancia es:

CONCLUSIÓN: “La distancia mínima desde el punto  hasta
hasta  es aproximadamente
es aproximadamente  ”
”
