Examen Parcial - cbc.28. Análisis Matemático I - 1° Cuatrimestre 2005
- Enunciado
  - Punto I
  - Punto II
  - Punto III
  - Punto IV
- Resolución
- Discusión

Examen Parcial - cbc.28. Análisis Matemático I - 1° Cuatrimestre 2005

Fecha: 1° Cuatrimestre 2005
Tema: 4

Esta página está incompleta; podés ayudar completando el material.

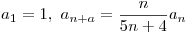Sea $<tex>a_n</tex>$ la sucesión dada en la forma recurrente por $<tex>a_1=1, \ a_{n+a}=\frac{n}{5n+4}a_n</tex>$ para todo $<tex>n\geq1</tex>$ . Calcule $<tex> \displaystyle \lim_{n\rightarrow \infty} \left( 4^na_n+3\sqrt[n]{5} \right)</tex>$ .

Punto II

Dada 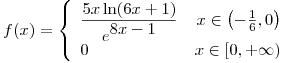$<tex> f(x)=\left\{ \begin{array}{lr}\displaystyle \frac{\displaystyle 5x\ln(6x+1)}{\displaystyle e^{\displaystyle 8x-1}} & x\in\left( -\frac{1}{6},0 \right)\\ 0 & x\in \left[ 0,+\infty \right) \end{array} \right.</tex>$ , analice, mediante el estudio del cociente incremental, la existencia de $<tex> f'(0)</tex>$ .

Punto III

Demuestre que la ecuación $<tex> -x^2+4=x\cos{x}-\sen{x}</tex>$ tiene exactamente dos soluciones, una positiva y una negativa.

Punto IV

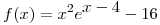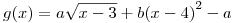Dadas las funciones $<tex> f(x)=\displaystyle x^2e^{\displaystyle x-4}-16</tex>$ y $<tex> g(x)=a\sqrt{x-3}+b{\left(x-4\right)}^2-a</tex>$ , determine $<tex> a</tex>$ y $<tex> b</tex>$ para que los dos polinomios de Taylor de orden $<tex> 2</tex>$ en $<tex> x=4</tex>$ de $<tex>f </tex>$ y de $<tex> g</tex>$ coincidan.

Resolución

Discusión

Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.