Tabla de Contenidos
Examen (Libre) - CBC 28. Análisis Matemático I - 18/07/08
Fecha: 1º Cuatrimestre 2008
Día: 18/07/2008
Enunciado
Punto I
Dada la funcion 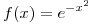 , si
, si 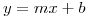 es la ecuacion de una recta tangente a
es la ecuacion de una recta tangente a  , describir como intervalo o union de intervalos al conjunto de los valores que puede tomar
, describir como intervalo o union de intervalos al conjunto de los valores que puede tomar  .
.
Punto II
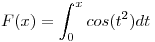
Aproximar 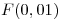 por el polinomio de Taylor de orden 1 en
por el polinomio de Taylor de orden 1 en  . Probar que el error cometido es
. Probar que el error cometido es 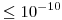 (se puede usar que
(se puede usar que 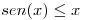 para todo
para todo 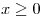 sin demostracion).
sin demostracion).
Punto III
 Hallar la cantidad de soluciones de la ecuacion
Hallar la cantidad de soluciones de la ecuacion 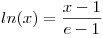 en
en ![<tex>[1;e]</tex> <tex>[1;e]</tex>](lib/plugins/latex/images/c965b61f34bf299f705bcaa9e8bf915d6c1efdf1_0.png) .
.
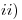 Usando el item anterior, calcular el area encerrada por
Usando el item anterior, calcular el area encerrada por  y
y 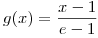 para
para 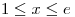 .
.
Punto IV
Hallar  derivable tal que
derivable tal que 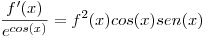 y
y 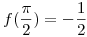
Punto V
Calcular todos los  tal que
tal que ![<tex>\sum^{\infty}_{n=1}n^p(\sqrt[2]{n^3+5}-\sqrt[2]{n^3+1})</tex> <tex>\sum^{\infty}_{n=1}n^p(\sqrt[2]{n^3+5}-\sqrt[2]{n^3+1})</tex>](lib/plugins/latex/images/204b103daf1cc803a7a9acdf0ec65dc0e38d1aec_0.png) converge.
converge.
Resolución
Discusión
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
