Tabla de Contenidos
Examen Parcial - 27 Álgebra I - 2005
Cátedra: Sede Drago
Fecha: 1º Cuatrimestre 2005
Enunciado
Punto I
Dados los planos  ,
, 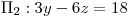 y
y 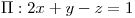 , hallar dos puntos
, hallar dos puntos 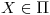 tales que
tales que 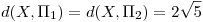 .
.
Punto II
Sean ![<tex>A= \left[ \begin{array}{ccc} 1 & 3 & 2\\ k & 0 & 1\\ 2 & 1 & 1\\ \end{array} \right]</tex> <tex>A= \left[ \begin{array}{ccc} 1 & 3 & 2\\ k & 0 & 1\\ 2 & 1 & 1\\ \end{array} \right]</tex>](lib/plugins/latex/images/58b0c67df2c610fe935ca4288e81b3ad65326984_0.png) y
y ![<tex>B= \left[ \begin{array}{ccc} k & 3 & 1\\ 5 & k & 0\\ 7 & k & 1\\ \end{array} \right]</tex> <tex>B= \left[ \begin{array}{ccc} k & 3 & 1\\ 5 & k & 0\\ 7 & k & 1\\ \end{array} \right]</tex>](lib/plugins/latex/images/34fb16bfbb7c8d12db2ff59ebf701402d4ab8b6f_0.png) . Hallar todos los valores de
. Hallar todos los valores de 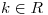 para los cuales el sistema
para los cuales el sistema 
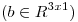 tiene solución única y el sistema
tiene solución única y el sistema 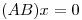 tiene infinitas soluciones.
tiene infinitas soluciones.
Punto III
Sea 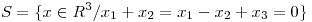 . Hallar una base B de
. Hallar una base B de  de modo qe la primera coordenada en base B se los vectores de
de modo qe la primera coordenada en base B se los vectores de  sea cero, y que las coordenadas del vector
sea cero, y que las coordenadas del vector 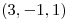 en la base B sean
en la base B sean 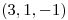 .
.
Punto IV
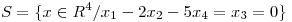 ,
, 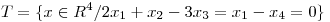 . Encontrar si es posible un subespacio
. Encontrar si es posible un subespacio 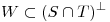 tal que
tal que 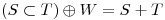 .
.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
