Examen (Parcial) - 27. Álgebra I - 19/11/08
Sede: Ciudad Universitaria/Turno Tarde
Fecha: Segundo Parcial - Primera Oportunidad - 2º Cuatrimestre 2008
Día: 19/11/2008
Enunciado
Punto I
Sea 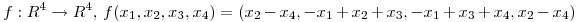
Definir, si es posible, un proyector 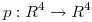 que verifique simultaneamente:
que verifique simultaneamente:
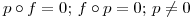
Punto II
Sean 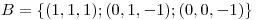 y
y 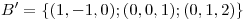 y sea
y sea 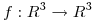 la transformación lineal tal que
la transformación lineal tal que 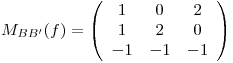
Dados 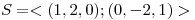 y
y 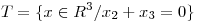 , hallar
, hallar 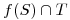
Punto III
Sea 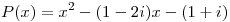 . Hallar un polinomio
. Hallar un polinomio ![<tex>Q(x) \in R[X]</tex> <tex>Q(x) \in R[X]</tex>](lib/plugins/latex/images/c370142b5a3f33724baee18013c38da23972f63f_0.png) , de grado mínimo, que tenga a 3 como raíz doble, y tal que todas las raices de P sean raices de Q.
, de grado mínimo, que tenga a 3 como raíz doble, y tal que todas las raices de P sean raices de Q.
Punto IV
Sean 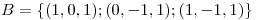 y
y 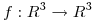 la t.l tal que
la t.l tal que 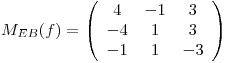
Hallar los autovalores y autovectores de  y decidir si
y decidir si  es diagonalizable.
es diagonalizable.
Resolución
Punto II
Busco 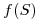 : uso que
: uso que 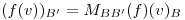
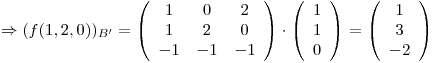
porque 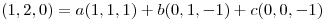
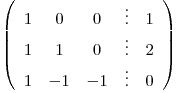 triangulo y obtengo
triangulo y obtengo 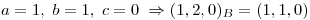
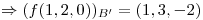
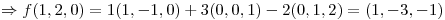
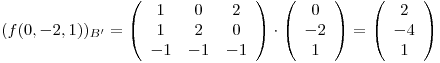
porque 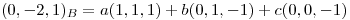
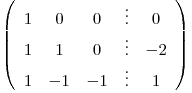 triangulo y obtengo
triangulo y obtengo 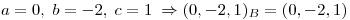
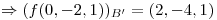
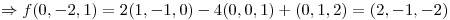
Busco 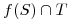


Busco que cumpla con la ecuación de 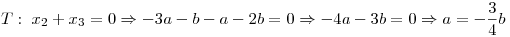
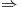 reemplazando obtengo
reemplazando obtengo 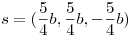
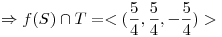
Punto III
Primero busco las raices de 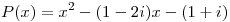
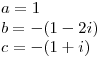
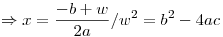
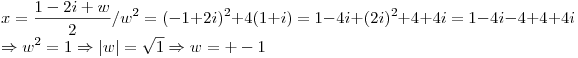
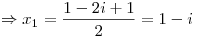 y
y 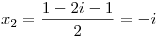
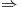 Raices de
Raices de 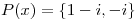 que a su vez tienen que ser raices de
que a su vez tienen que ser raices de 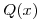 .
.
Como ![<tex>Q(x) \in R[X]</tex> <tex>Q(x) \in R[X]</tex>](lib/plugins/latex/images/c370142b5a3f33724baee18013c38da23972f63f_0.png) , si
, si 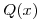 tiene una raíz compleja, entonces, el conjugado de esta también es raíz de
tiene una raíz compleja, entonces, el conjugado de esta también es raíz de 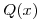
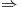 raices de
raices de 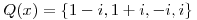
Además, 3 tiene que ser raíz doble.
Punto IV
Primero busco la matríz de la t.l expresada en una sola base
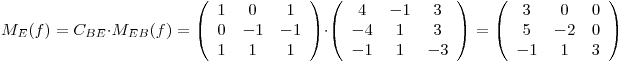
Busco los autovalores de f, para eso necesito 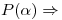 busco
busco 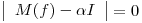
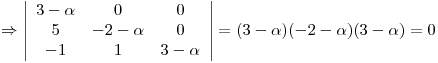 (desarrollando el determinante por la primer fila)
(desarrollando el determinante por la primer fila)
 autovalores de
autovalores de 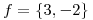
Si 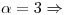 busco
busco 
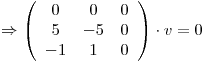
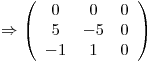

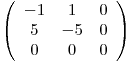
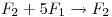
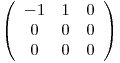
 Busco
Busco 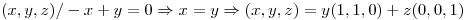
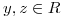
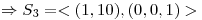
Como 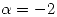 es raíz simple
es raíz simple 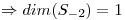 ya puedo asegurar que
ya puedo asegurar que  es diagonalizable.
es diagonalizable.
Si 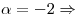 busco
busco 
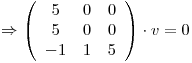
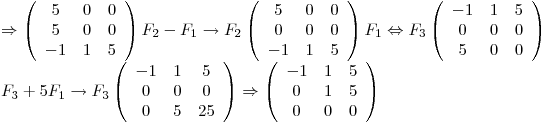
Busco 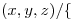
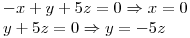

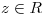
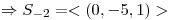
Efectivamente tengo una base de autovectores 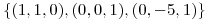
 es diagonalizable.
es diagonalizable.
