Examen (Parcial) - 27. Álgebra I - 08/10/08
Sede: Ciudad Universitaria/turno tarde
Fecha: Primer Parcial, Primera Oportunidad - 2° Cuatrimestre 2008
Día: 08/10/2008
Enunciado
Punto I
Sean el plano 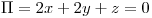 , la recta
, la recta 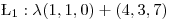 y
y  la recta que pasa por
la recta que pasa por 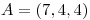 y
y 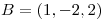 .
Hallar, si existe, una recta L que verifique simultaneamente
.
Hallar, si existe, una recta L que verifique simultaneamente  ;
; 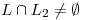 ,
, 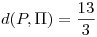
Punto II
Dado el sistema que tiene matriz ampliada 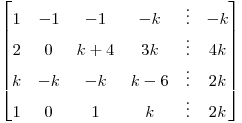 , hallar todos los valores de
, hallar todos los valores de 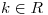 para los cuales el sistema tiene infinitas soluciones.
Para alguno de los valores hallados resolver completamente el sistema.
para los cuales el sistema tiene infinitas soluciones.
Para alguno de los valores hallados resolver completamente el sistema.
Punto III
Sean 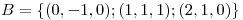 y
y 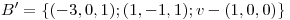 bases de
bases de 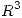 Hallar
Hallar 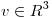 sabiendo que
sabiendo que 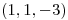 tiene las mismas coordenadas en las dos bases.
tiene las mismas coordenadas en las dos bases.
Punto IV
Sean 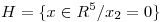 ,
, 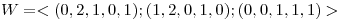 y
y 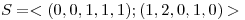 .
Hallar, si es posible, un subespacio
.
Hallar, si es posible, un subespacio 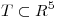 que satisfaga simultáneamente:
que satisfaga simultáneamente:
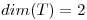 ;
; 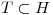 ;
; 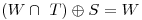
Resolución
Punto I
Busco la recta  que pasa por los puntos A y B:
que pasa por los puntos A y B:
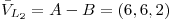
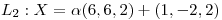
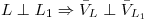
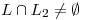 entonces ambas rectas se tienen que cortas en algún punto; puedo pedir que
entonces ambas rectas se tienen que cortas en algún punto; puedo pedir que 
Además, para que 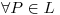 la distancia a
la distancia a  sea constante,
sea constante, 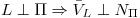 Uso
Uso 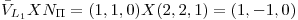 (cumple con las condiciones anteriores)
(cumple con las condiciones anteriores)
Como 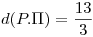 , si
, si 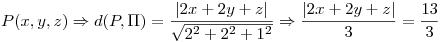
Obtengo dos planos: 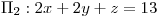 y
y 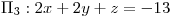 Esto quiere decir que a la distancia dada de
Esto quiere decir que a la distancia dada de  hay dos planos paralelos a este. La recta que busco va a estar incluida en alguno de estos.
hay dos planos paralelos a este. La recta que busco va a estar incluida en alguno de estos.
Pido que se cumpla 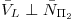
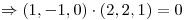 se verifica.
se verifica.
Además necesito un punto de paso de L que cumpla con la ecuación del plano y que me sirva para garantizar 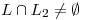 Busco
Busco 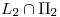
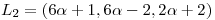 punto genérico de
punto genérico de  que cumpla con la ecuación de
que cumpla con la ecuación de 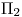
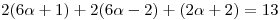 aplicando distributiva y agrupando
aplicando distributiva y agrupando
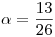
Remplazando en el punto genérico obtengo que 
Una posible recta que cumple con todo lo pedido es 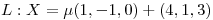
Punto III
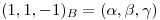
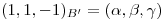 ya que las coordenadas en ambas bases son las mismas.
ya que las coordenadas en ambas bases son las mismas.
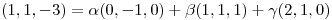
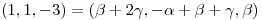 armo la matriz con los vectores como columnas para triangular y resolver el sistema.
armo la matriz con los vectores como columnas para triangular y resolver el sistema.
Obtengo 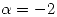 ,
,  ,
, 
Verifico:
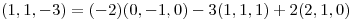
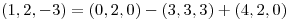

Usando las coordenadas obtenidas y la base B' despejo  :
:
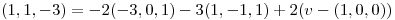
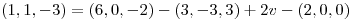
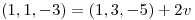
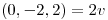
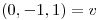
Punto IV
Generadores de 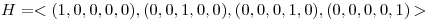
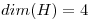
Los vectores de  son l.i, sirven como base
son l.i, sirven como base 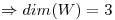
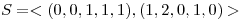 los vectores de
los vectores de  son l.i, sirven como base
son l.i, sirven como base 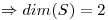
Usando el teorema de la dimensión:
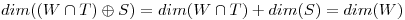
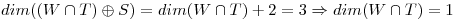
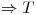 solo va a compartir un vector con
solo va a compartir un vector con  para que
para que 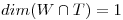
Además como 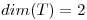 y
y 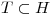 , el otro vector de
, el otro vector de  que me falta tiene que estar incluido en
que me falta tiene que estar incluido en 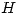 y ser l.i con los vectores de
y ser l.i con los vectores de  para que se siga cumpliendo
para que se siga cumpliendo 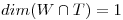
Busco  : los vectores de
: los vectores de  son de la forma:
son de la forma:
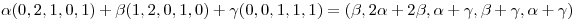
Tienen que cumplir con la ecuación de 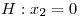
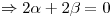


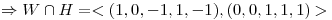
Si uso 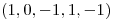 como uno de los vectores de
como uno de los vectores de  garantizo
garantizo 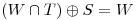 ya que es l.i con los vectores de
ya que es l.i con los vectores de 
Si tomo 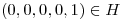 es l.i con el otro vector de
es l.i con el otro vector de 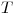
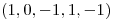 (el cual a su vez está en
(el cual a su vez está en  y entonces está en
y entonces está en  y en
y en 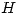
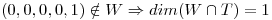
Un posible  es:
es: 
