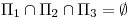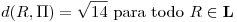Tabla de Contenidos
Examen Parcial - 27. Álgebra I - 17/05/2006
Sede: Ciudad Universitaria/Turno Mañana
Fecha: Primer Parcial, Primera Oportunidad - 1° Cuatrimestre 2006
Día: 17/05/2006
Esta página está incompleta; podés ayudar completando el material.
Enunciado
Punto I
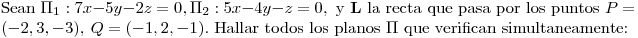
Punto II
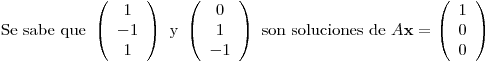
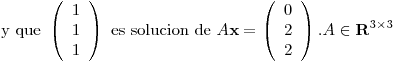

Punto III
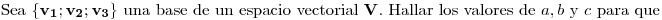
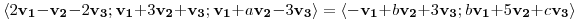
Punto IV
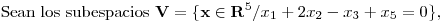

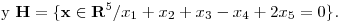
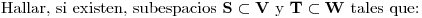

Resolución
Punto I
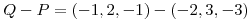
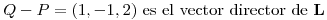
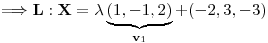
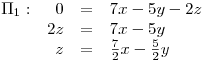
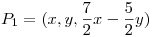
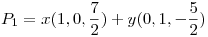
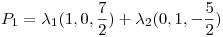
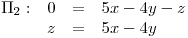
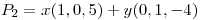
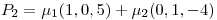
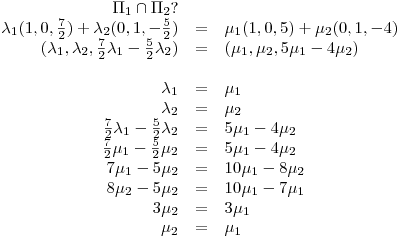
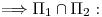
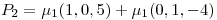
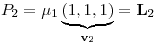
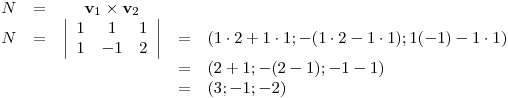
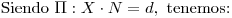
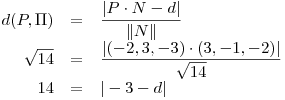
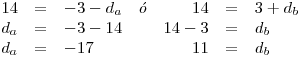
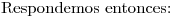

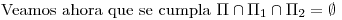
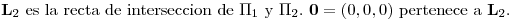
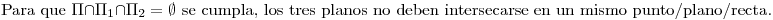
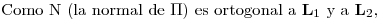
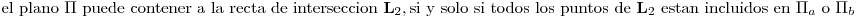 .
.
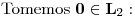

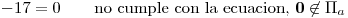
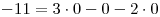
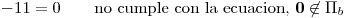
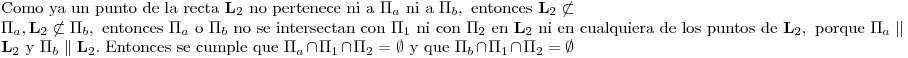
Punto II
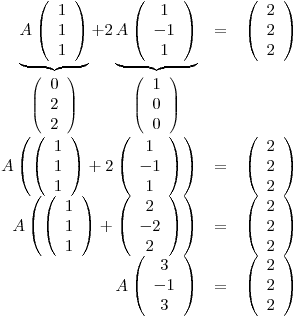
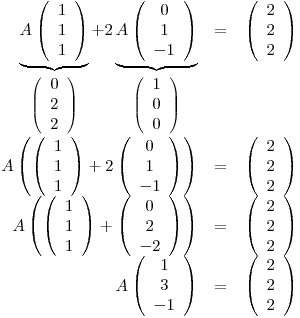
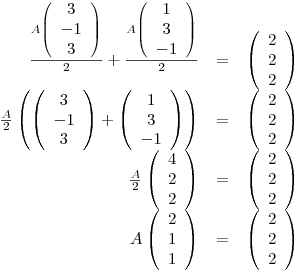
Punto III
Punto IV
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported