[[Enunciado]]
Enunciado
Ejercicio 1: En 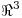 los subespacios
los subespacios 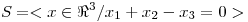 y
y 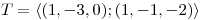 . Hallar
. Hallar  de
de 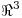 tal que:
tal que:
I) coordenadas en B de S tengan la forma (a,b,0)
II) coordenadas en B de T tengan la forma (0,c,d)
III) coordenadas en b de (1,3,2) son (2,-1,1)
Ejercicio 2: Sea 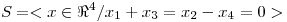 . Hallar T perteneciente a a
. Hallar T perteneciente a a 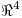 tal que:
tal que:
I)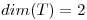
II) 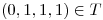
III) T intersección S distinto de <0>
IV) T ortogonal intersección S distinto de <0>
Ejercicio 3: 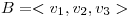
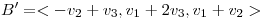 bases de
bases de 
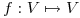 una T.L. tal que:
una T.L. tal que:
![<tex>M_{b'b}(f) = \left[\begin{array}{ccc}2 & 2 & -1\\1 & 3 & 1\\3 & 5 & 0\end{array}\right]</tex> <tex>M_{b'b}(f) = \left[\begin{array}{ccc}2 & 2 & -1\\1 & 3 & 1\\3 & 5 & 0\end{array}\right]</tex>](lib/plugins/latex/images/181f19c8b50065a56d665339f620ce0173646aee_0.png)
y 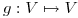 un isomorfismo tal que:
un isomorfismo tal que:
![<tex>M_b(g \circ f) = \left[\begin{array}{ccc}1 & -3 & 4\\0 & 1 & -1\\2 & -1 & 3\end{array}\right]</tex> <tex>M_b(g \circ f) = \left[\begin{array}{ccc}1 & -3 & 4\\0 & 1 & -1\\2 & -1 & 3\end{array}\right]</tex>](lib/plugins/latex/images/29a89a34f88ad5ae12af59abd3f689fc5b809edc_0.png)
Hallar  tal que
tal que 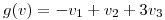
Ejercicio 4: En 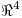 ;
; 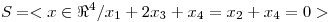 y
y 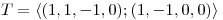 . Definir una TL
. Definir una TL  tal que:
tal que:
I) 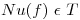
II) 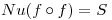
III) 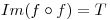
Ejercicio 5: 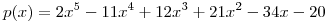 Hallar todas las raíces sabiendo que la suma de tres de sus raíces da 3/2 y el producto de las mismas da 2.
Hallar todas las raíces sabiendo que la suma de tres de sus raíces da 3/2 y el producto de las mismas da 2.
Resolución
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
