Examen Parcial - 76.56. Instrumentación y Control - 26/05/2008
Cátedra: Zanini
Fecha: Segunda Oportunidad - Primer Cuatrimestre 2008
Día: 26/05/2008
Enunciado
Punto 1
Para calentar un producto, se dispone de un intercambiador de calor con un líquido calefactor de densidad 1 en la camisa. Por experiencia previa se conoce que la función de transferencia que relaciona la temperatura de salida del caudal de proceso con el caudal del calefactor es de primer orden. para determinar la función de trnasferencia del intercambiador, se movió en forma inmediata la válvula de 50% a 55%.
La válvula es lineas y tiene un Cv máximo de 130. El fluido se encuentra aguas arriba de la válvula a 50 psig constantes. El colector de retorno del fluido está a una presión fija de 21 psig. La pérdida de carga en el intercambiador con la válvula un 50% abierta es de 18 psig.
Considerar que la pérdida de carga en el intercambiador es proporcional al cuadrado del caudal.
Midiendo la temperatura de salida se obtuvo el siguiente resultado:
| Tiempo (seg) | 0 | 5 | 10 | 15 | 20 | 30 | 40 | 60 | 80 |
|---|---|---|---|---|---|---|---|---|---|
| Temp. salida (ºC) | 70 | 72.73 | 74.52 | 75.7 | 76.5 | 77.34 | 77.7 | 77.95 | 78 |
a) Determinar la función de transferencia del intercambiador tal que relacione la temperatura de salida con el caudal del fluido calefactor.
b) La válvula de control tiene una entrada de 4-20mA con una dinámica desestimable y el elemento de medición se instala aguas abajo (tal que transcurren 5 seg entre que el fluido sale del intercambiador y llega al punto de medición) con una dinámica desestimable y una calibración 4-20 mA para un rando 50ºC-100ºC. Determinar la función de transferencia entre la entrada de la válvula de control y la salida del elemento de medición para el estado estacionario de la válvula abierta al 50%.
Determinar la función de transferencia A LAZO ABIERTO que relacione la señal de salida del elemento de medición de temperatura con la señal enviada a la válvula de control indicando las unidades de cada uno de los parámetros.
c) Realizar el diagrama de Bode cualitativo para la FT obtenida en el punto b.
Punto 2
Para evitar variaciones en la temperatura de entrada a un reactor, se utiliza un tanque compensador adiabático de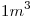 
. El caudal es constante e igual a 100 litros/min. En estado estacionario, la temperatura del reactivo es de 72ºC y sale del reactor con una concentración de 0.3 M. La conceentración de entrada es igual en todo momento a 1M. Se sabe que el reactor tiene una dinámica que relaciona la concnetración de salida con la temperatura de entrada al reactor de primer orden con T=7min y K=-0.01M/ºC.
Se espero que por razones del proceso aguas arriba la temperatura de entrada al tanque compensador suba a 80ºC durante 4 minutos. Luego vuelve a 72ºC.
- Indicar la mínima concentración de salida que se obtendrá.
- Indicar la concentración de salida 15 minutos después de la perturbación.
- Graficar cualitativamente la evolución de la temperatura de salida del tanque y del reactor en un mismo gráfico.
Punto 2
Resolución
Punto 1
OJO observar que 
a veces se refiere a “segundos” y a veces a la variable de Laplace.
a)
Como para 
en la válvula se tiene 
, entonces:
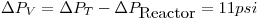
Si ahora se plantea para la pérdida en el intercambiador:
La C equivalente es:
Lo calculo para 55% de Cv: 
Entonces: 
Ahora ya conozco el salto de Q que hubo en el ensayo. Para conocer el salto de T se observa en los datos de la table que si se grafican se ve que se acerca “asintóticamente” a 78ºC, que será la temperatura final.
El T de la función de transferencia se calcula con la tabla:
b)
Se puede pensar el sistema como una unión de bloques:
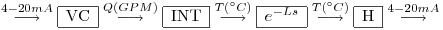
La válvula de control tiene una dinámina desestimable, es decir que es sólo una ganancia (la inherente):
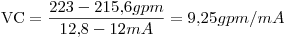
Para el intercambiador era (del a)):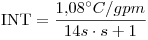 
La ganancia del transmisor es la de la calibración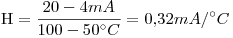 
Entonces la función de transferencia total se obtiene multiplicando:
Punto 2
INCOMPLETO
