75.31. Teoría de lenguaje - Ejercicios Resueltos
Estos ejercicios pertenecen al libro Concepts, Techniques, and Models of Computer Programming, escrito por Peter Van Roy y Seif Haridi.
Capítulo 1 - Introduction to Programming Concepts
Ejercicio 1 - A calculator
Enunciado
Section 1.1 uses the system as a calculator. Let us explore the possibilities:
- Calculate the exact value of
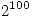 without using any new functions. Try to think of shortcuts to do it without having to type
without using any new functions. Try to think of shortcuts to do it without having to type 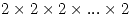 with one hundred 2s. Hint: use variables to store intermediate results.
with one hundred 2s. Hint: use variables to store intermediate results. - Calculate the exact value of
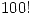 without using any new functions. Are there any possible shortcuts in this case?
without using any new functions. Are there any possible shortcuts in this case?
Resolución
Se puede simplificar de varias maneras.
V1=2*2*2*2*2
V2=V1*V1*V1*V1*V1
V3=V2*V2*V2*V2
{Browse V3}
Matemáticamente sería: 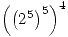
Ejercicio 9 - Memory store
Enunciado
Th is exercise investigates another way of introducing state: a memory store. The memory store can be used to make an improved version of FastPascal that remembers previously calculated rows.
Punto c
We have given the memory store as a library. It turns out that the memory store can be defined by using a memory cell. We outline how it can be done and you can write the definitions. The cell holds the store contents as a list of the form ![<tex>[N_1|X_1 ... N_n|X_n]</tex> <tex>[N_1|X_1 ... N_n|X_n]</tex>](lib/plugins/latex/images/799ce2ca0f1f3b152fdbb5e01707dbd41cceea7c_0.png) , where the cons
, where the cons 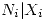 means that cell number
means that cell number 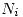 has content
has content 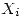 .This means that memory stores, while they are convenient, do not introduce any additional expressive power over memory cells.
.This means that memory stores, while they are convenient, do not introduce any additional expressive power over memory cells.
Resolución
Punto c
declare NewStore Size Put Get
fun {NewStore}
{NewCell nil}
end
fun {Size S}
fun {SizeAuxiliar S}
fun {Max X Y} if X>Y then X else Y end end
in
case S of [H1 T1]|T then
{Max H1 {SizeAuxiliar T}}
else
0
end
end
in
{SizeAuxiliar @S}
end
proc {Put S N E}
fun {PutAuxiliar S N E}
case S of [H1 T1]|T then
if H1==N then
[H1 E]|T
else
[H1 T1]|{PutAuxiliar T N E}
end
else
[N E]|S
end
end
in
S:={PutAuxiliar @S N E}
end
fun {Get S N}
fun{GetAuxiliar S N}
case S of [H1 T1]|T then
if H1==N then
T1
else
{GetAuxiliar T N}
end
else
nil
end
end
in
{GetAuxiliar @S N}
end
S={NewStore}
{Put S 1 [1 3 5]}
{Put S 2 454}
{Put S 3 [777 888]}
{Put S 7 'vanRoy'}
{Browse {Size S}}
{Browse {Get S 1}}
{Browse {Get S 2}}
{Browse {Get S 3}}
{Browse {Get S 4}}
