Examen Final - 75.15. Base de Datos - 12/08/2009
Cátedra: Ale (catedra unica)
Fecha: 2° Oportunidad - (2° Cuatrimestre) 2008
Día: 12/08/2009
Enunciado
Ejercicio I
Mostrar que 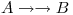 y
y 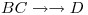 implican
implican 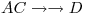 usando el tableau y el metodo chase para
usando el tableau y el metodo chase para ![<tex>R=[A,B,C,D,E]</tex> <tex>R=[A,B,C,D,E]</tex>](lib/plugins/latex/images/16aa1789a7c846ec351255edb4b934e68ee78574_0.png)
Ejercicio II
Estimar el tamaño de R(AB)|x|S(BC) si se cuenta con el siguiente histograma
| B<0 | B=0 | B>0 | |
|---|---|---|---|
| R | 500 | 100 | 400 |
| S | 300 | 200 | 500 |
Asumir que existen 100 valores diferenties de B<0 y 200 valores de B>0
Ejercicio III
Dada la tabla Notas:
| Estudiante | Nota_BD | Nota_SII |
|---|---|---|
| A | 4 | Null |
| B | Null | 9 |
| C | 10 | 8 |
La consulta:
SELECT Estudiante FROM Notas
WHERE (Nota_BD > Nota_SII
AND Nota_SII > 7
AND Nota_BD > 9 )
OR ( Nota_BD < 5)
Da como resultado:
- B y C Solamente
- A y C solamente
- A
- A, B y C
Elegir la respuesta correcta y justificar
Ejercicio IV
Sabiendo que el algoritmo de recuperacion (creacion de logs? no recuerdo) es UNDO/REDO, demostrar los registros que se generaron en el LOG. Valores iniciales:
- salario = 1
- tax = 2
| N° | Transaccion 1 | Transaccion 2 | Transaccion 3 |
|---|---|---|---|
| 1 | Start | ||
| 2 | Read tax | ||
| 3 | tax=tax+1 | ||
| 4 | Start | ||
| 5 | Read Salario | ||
| 6 | salario = salario+1 | ||
| 7 | Write tax | ||
| 8 | commit | ||
| 9 | start | ||
| 10 | Read tax | ||
| 11 | Read salario | ||
| 12 | tax= …(no copie mas) | ||
| 13 | |||
| 14 | |||
| 15 | |||
| 16 |
Esta tabla esta incompleta; no llegue a terminar de copiarla... A ver si alguien la puede completar.
Resolución
Ejercicio I
Como busco demostrar que 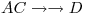 es implicada por
es implicada por 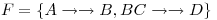 divido
divido  en
en ![<tex>R1=[ACD]</tex> <tex>R1=[ACD]</tex>](lib/plugins/latex/images/5259f67a4fb4c8f17663f454fd5ee547948a74fa_0.png) y
y ![<tex>R2=[ABCE]</tex> <tex>R2=[ABCE]</tex>](lib/plugins/latex/images/ecc5536cf39f6edac296516b2cfc74257696687d_0.png) haciendo uso de la propiedad que indica que la descomposición de
haciendo uso de la propiedad que indica que la descomposición de 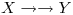 se puede descomponer en
se puede descomponer en  y
y 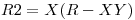 .
.
| A | B | C | D | E | |
|---|---|---|---|---|---|
| R1 |  | 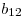 | 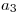 | 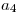 | 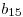 |
| R2 |  | 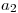 | 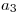 | 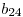 | 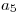 |
Ahora, para demostrar que 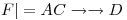 , usando el conjunto de dependencias
, usando el conjunto de dependencias  tendría conseguir una fila que tenga todas las variables distinguidas.
tendría conseguir una fila que tenga todas las variables distinguidas.
La dmv 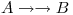 se transforma en una dependencia de junta
se transforma en una dependencia de junta ![<tex>|x|[ AB ; ACDE]</tex> <tex>|x|[ AB ; ACDE]</tex>](lib/plugins/latex/images/9adfa9890fac36b6b11729f15eeab9c58236b2ff_0.png)
Por lo que si ahora proyectamos sobre cada conjunto de la junta obtenemos:
- Por
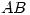
| A | B |
|---|---|
 | 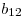 |
 | 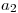 |
- Por
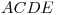
| A | C | D | E |
|---|---|---|---|
 | 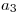 | 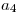 | 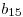 |
 | 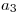 | 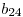 | 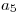 |
Si hacemos la junta de estas dos tablas, obtenemos las filas:
| A | B | C | D | E |
|---|---|---|---|---|
 | 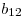 | 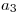 | 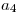 | 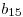 |
 | 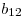 | 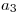 | 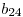 | 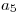 |
 | 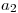 | 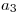 | 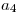 | 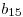 |
 | 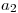 | 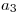 | 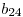 | 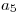 |
Pero como las filas 1 y 4 ya están en el tableau, no las agrego, por lo que ahora me queda:
| A | B | C | D | E | |
|---|---|---|---|---|---|
| R1 |  | 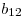 | 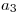 | 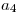 | 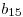 |
| R2 |  | 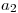 | 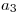 | 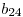 | 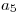 |
Agregada por 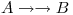 |  | 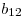 | 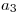 | 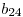 | 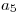 |
Agregada por 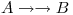 |  | 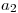 | 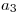 | 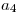 | 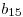 |
La dmv 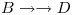 se transforma en una dependencia de junta
se transforma en una dependencia de junta ![<tex>|x|[ BD ; ABCE]</tex> <tex>|x|[ BD ; ABCE]</tex>](lib/plugins/latex/images/341212e9133e58a8986c1d2e08fdb2f5b31f9120_0.png) , por lo que si hacemos lo mismo que antes nos quedan las proyecciones:
, por lo que si hacemos lo mismo que antes nos quedan las proyecciones:
- Por
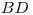
| B | D |
|---|---|
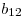 | 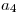 |
 | 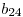 |
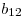 | 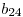 |
 | 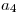 |
- Por

| A | C | D | E |
|---|---|---|---|
 | 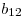 | 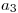 | 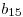 |
 |  | 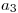 | 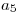 |
 | 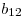 | 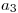 | 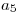 |
 |  | 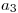 | 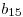 |
Al hacer la junta de estas dos tablas, en particular la fila 4 de la primera con la 2 de la segunda, va a aparecer una fila con todos los valores distinguidos:
 |  |  | 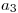 | 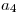 | 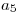 |
Ejercicio II
Para estimar el tamaño de esa junta tenemos que calcular cada rango por separado y sumarlos:
- Para
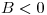 :
:
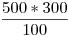
- Para
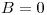 :
:

- Para
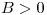 :
:
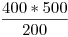
Entonces nos queda:
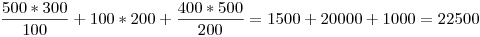
Ejercicio III
La respuesta es “A y C solamente”.
