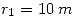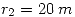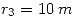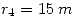Trabajo Práctico Número 1 - Ecuaciones no lineales
Consignas
La Figura 1 muestra un mecanismo de 4 barras articuladas.
El ángulo 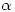 es el parámetro de entrada, mientras que
es el parámetro de entrada, mientras que  es la variable de salida. La relación entre
es la variable de salida. La relación entre 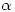 y
y  puede obtenerse a partir del planteo de la ecuación que surge al considerar la estructura como un lazo cerrado.
puede obtenerse a partir del planteo de la ecuación que surge al considerar la estructura como un lazo cerrado.
Teniendo en cuenta los siguientes valores:
Se pide:
- A partir de la ecuación obtener la realción entre
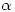 y
y  (planteando las ecuaciones para “x” y para “y”).
(planteando las ecuaciones para “x” y para “y”). - Encontrar las posiciones límites del sistema.
- Plantear el método de Newton Raphson y veri…car las condiciones de convergencia.
- Implementar el Método de Newton-Raphson en un programa computacional en alguno de los siguientes lenguajes: FORTRAN, C, Pascal, Basic, MATLAB.
- Desarrollar una tabla con los valores
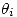 tomando como parámetros de entrada
tomando como parámetros de entrada 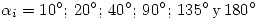
- Conclusiones
Resolución
Obtención de las ecuaciones que relacionan los ángulos
Para poder plantear las ecuaciones, llamamos al ángulo que forma la barra 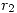 con una recta para lela a
con una recta para lela a 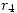 ,
, 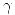 .
.
Planteamos primero las ecuaciones en el eje x:
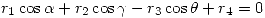
Planteamos también para el eje y:
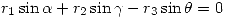
Despejando todo en función de 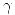 y usando que la suma de los cuadrados da uno llegamos a:
y usando que la suma de los cuadrados da uno llegamos a:
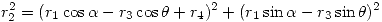
Distribuyendo los cuadrados y reordenando:
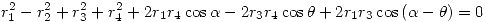
Entonces esta es la función que relaciona alpha y theta, y es la que vamos a utilizar para obtener las raices por Newton-Raphson.
El programa utilizado “angulos.m” se detalla a continuación:
%angulos.m
%Trabajo Practico de A.Numerico1
clear
R=input('ingrese [r1 r2 r3 r4]= ');
r1=R(1); r2=R(2); r3=R(3); r4=R(4);
a=input('ingrese el valor de alpha(degrees): ');
a=a*pi/180;
tol=0.5e-7;
x(1)=pi/2+0.3;
x(2)=x(1)- func(a,x(1),r1,r2,r3,r4)/dfunc(a,x(1),r1,r2,r3,r4);
i=2;
while abs(x(i)-x(i-1))>tol & abs( func(a,x(i),r1,r2,r3,r4)-func(a,x(i-1),r1,r2,r3,r4) )>tol;
i=i+1;
x(i)=x(i-1)-func(a,x(i-1),r1,r2,r3,r4)/dfunc(a,x(i-1),r1,r2,r3,r4);
end
d1=x.*(180/pi);
disp('La solucion es: ');
d1
Donde las funciones func y dfunc son:
function F=func(alpha,theta,r1,r2,r3,r4); %Esta funcion sera la que debemos hallar el cero para un valor fijo de alpha A1=r1^2-r2^2+r3^2+r4^2; A2=-2*r1*r3*cos(alpha)*cos(theta); A3=-2*r1*r3*sin(alpha)*sin(theta); A4=2*r1*r4*cos(alpha); A5=-2*r3*r4*cos(theta); F=A1+A2+A3+A4+A5;
function DF=dfunc(alpha,theta,r1,r2,r3,r4); %es la derivada parcial con respecto a theta B1=2*r1*r3*cos(alpha)*sin(theta); B2=-2*r1*r3*sin(alpha)*cos(theta); B3=2*r3*r4*sin(theta); DF=B1+B2+B3;
La corrida del programa para los valores de alpha pedidos se detalla a continuación:
>> angulos ingrese [r1 r2 r3 r4]= [10 20 10 15] ingrese el valor de alpha(degrees): 10 La solucion es: d1 = 107.1887 55.9060 53.9903 53.9641 53.9641 53.9641
>> angulos ingrese [r1 r2 r3 r4]= [10 20 10 15] ingrese el valor de alpha(degrees): 20 La solucion es: d1 = 107.1887 61.7448 59.4865 59.4523 59.4522 59.4522
>> angulos ingrese [r1 r2 r3 r4]= [10 20 10 15] ingrese el valor de alpha(degrees): 40 La solucion es: d1 = 107.1887 74.8363 73.1077 73.0915 73.0915
>> angulos ingrese [r1 r2 r3 r4]= [10 20 10 15] ingrese el valor de alpha(degrees): 90 La solucion es: d1 = 107.1887 120.0186 119.7142 119.7141 119.7141
>> angulos ingrese [r1 r2 r3 r4]= [10 20 10 15] ingrese el valor de alpha(degrees): 135 La solucion es: d1 = 107.1887 188.8166 193.1599 193.4535 193.4549 193.4549
>> angulos ingrese [r1 r2 r3 r4]= [10 20 10 15] ingrese el valor de alpha(degrees): 180 La solucion es: d1 = Columns 1 through 7 107.1887 254.3948 106.8039 254.0925 106.5843 253.9232 106.4593 Columns 8 through 14 253.8278 106.3884 253.7741 106.3482 253.7437 106.3255 253.7265 Columns 15 through 21 106.3126 253.7168 106.3053 253.7114 106.3012 253.7083 106.2988 Columns 22 through 28 253.7065 106.2975 253.7055 106.2968 253.7049 106.2963 253.7046 Columns 29 through 35 106.2961 253.7044 106.2960 253.7043 106.2959 253.7043 106.2958 Columns 36 through 42 253.7042 106.2958 253.7042 106.2958 253.7042 106.2958 253.7042 Columns 43 through 49 106.2958 253.7042 106.2958 253.7042 106.2958 253.7042 106.2958 Columns 50 through 56 253.7042 106.2958 253.7042 106.2958 253.7042 106.2958 253.7042 Columns 57 through 63 106.2958 253.7042 106.2958 253.7042 106.2958 253.7042 106.2958 Columns 64 through 65 253.7042 106.2958
Observación: Se puede observar que para el valor de 135º, el programa converge hacia una solución mayor que 180º que no es físicamente posible, y para 180º el programa oscila sin converger.
Conclusiones y evaluación de la convergencia del método
Las condiciones de convergencia del método de Newton son las siguientes:
- F(x) continua en un intervalo dado y debe cambiar de signo en dicho intervalo para asegurar que ahí hay una raíz.
- La derivada no debe anularse en ese intervalo, se podría anular en el caso de que hubiera raíces múltiples y converger igual.
- La derivada segunda debe ser o positiva o negativa en todo el intervalo y para asegurar la convergencia se debe elegir un punto inicial en el cual el signo de la función sea igual al signo de la derivada segunda, para asegurar la convergencia y que no se escape de rango.
En nuestro caso el análisis convergencia, al ser dificultoso el análisis de la función de Newton, lo vamos a hacer con el gráfico de la función de Newton en función de theta para algunos valores de alpha fijos:
Como vemos en el gráfico para todos los valores de alpha entre 0º y 110º aproximadamente la función converge, para valores mayores a 135º la función queda por debajo del eje X por lo que no hay raíces.
Para los demás valores la función como vemos es continua, tiene una raíz, un intervalo adecuado podría ser entre theta igual a 0º y 180º y un valor adecuado a tomar de valor inicial podría ser 90 º ya que se encuentra en un punto donde la función va a converger para la raíz que nos interesa que es entre 0º y 180º , (theta no puede ser mayor a 180º ya que nuestro límite para r3 es el piso). De los máximos de las funciones los 90º esta a la izquierda y de los mínimos a la derecha por lo que esto va a orientar a la correcta convergencia.
Como acabamos de expresar la función presenta máximos o mínimos dependiendo del valor fijo de alpha para mi intervalo, es decir que la derivada primera se anula, pero eso no altera la convergencia ya que como vimos y probamos la función converge, lo que si tenemos que tener en cuenta es la condición inicial a tomar. Para cada función con un alpha distinto en las seguidas iteraciones al partir de 90º no pasa por un valor en el que se anule la derivada, por lo que no se anula el denominador de mi función de newton en ningún caso.
Entonces un rango adecuado sería: theta entre 0º y 180º
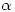 fijo entre 0º y 130º
fijo entre 0º y 130º
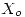 90º aprox.
90º aprox.
Con estas condiciones la función converge y a los valores aceptables del sistema (no puede dar un theta mayor a 180º por límites mismos de la estructura)