Examen Parcial - 75.12. Análisis Numérico
Cátedra: Amura
Fecha: Primera Oportunidad - Primer Cuatrimestre 2006
Día: 26/05/2006
Enunciado
Ejercicio I
Explique por qué los métodos de la bisección y de la “régula-falsi” (o de falsa posición) no pueden aplicarse a la ecuación 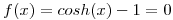 , aún sabiendo que hay una raíz en
, aún sabiendo que hay una raíz en  . Justifique su respuesta. (1.5 puntos)
. Justifique su respuesta. (1.5 puntos)
Ejercicio II
Explique las ventajas de utilizar el método baricéntrico de Lagrange y aplíquelo para obtener un valor de 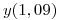 interpolando con un polinomio de grado dos o superior, con los datos de la siguiente tabla. Trabaje con cuatro decimales. (2.5 puntos)
interpolando con un polinomio de grado dos o superior, con los datos de la siguiente tabla. Trabaje con cuatro decimales. (2.5 puntos)
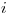 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
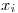 | 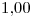 | 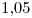 | 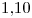 | 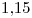 |
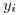 | 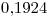 | 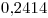 | 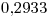 | 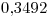 |
Ejercicio III
Indique si la siguiente afirmación es verdadera o falsa: “Los métodos de la régula falsi y de la secante para obtener raíces de ecuaciones convergen a la misma velocidad”. Justifique su respuesta. (2.5 puntos)
Ejercicio IV
Resuelva el siguiente sistema de ecuaciones lineales, aplicando el método más conveniente (directo o iterativo). Trabaje con cinco decimales y justifique su elección. (3.5 puntos)
![<tex>\left[ \begin{array}{cccc} 4533 & -1813 & -1700 & -340\\ -1813 & 4533 & 340 & 1700\\ -1700 & 340 & 7933 & -6913\\ -340 & 1700 & -6913 & 7933\end{array} \right]\left[ \begin{array}{c} x_1 \\ x_2 \\ x_3\\ x_4\end{array} \right]= \left[ \begin{array}{c} 0 \\ 0 \\ 0\\ -1.40000\end{array} \right]</tex> <tex>\left[ \begin{array}{cccc} 4533 & -1813 & -1700 & -340\\ -1813 & 4533 & 340 & 1700\\ -1700 & 340 & 7933 & -6913\\ -340 & 1700 & -6913 & 7933\end{array} \right]\left[ \begin{array}{c} x_1 \\ x_2 \\ x_3\\ x_4\end{array} \right]= \left[ \begin{array}{c} 0 \\ 0 \\ 0\\ -1.40000\end{array} \right]</tex>](lib/plugins/latex/images/fe068b35a3c2828560798cebeef6e373af62503c_0.png)
Resolución
Ejercicio I
Las condiciones para aplicar el método de la bisección son:
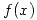 continua en el intervalo
continua en el intervalo 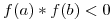
Las condiciones para aplicar el método de la régula falsi son:
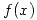 continua en el intervalo
continua en el intervalo 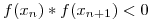
En la función dada, no se va a dar la segunda condición ya que 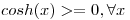 , lo que impide que la multiplicación de dos imágenes de la misma sea negativa.
, lo que impide que la multiplicación de dos imágenes de la misma sea negativa.
Ejercicio II
La ventaja de usar el método de Baricéntrico de Lagrange es que es más estable que sólo Lagrange (aunque no tanto como Newton). Además, este método permite agregar un nuevo punto fácilmente, así como cambiar el vector imágen rápidamente.
Ejercicio III
La afirmación es falsa, ya que el método de Régula Falsi es de arranque, por lo que su convergencia es lenta frente al de la secante que es de refinamiento iterativo.
Ejercicio IV
Dado que A es simétrica, no es diagonal dominante y es densa, conviene utilizar algún método directo como Choleski, Gauss o LU.
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá o mándame un mail GK
