Examen Parcial - 75.12. Análisis Numérico
Cátedra: Morelli
Fecha: Primera Oportunidad - Primer Cuatrimestre 2006
Día: 23/05/2006
Enunciado
Ejercicio 1
Sea el siguiente sistema de ecuaciones no lineales:
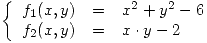
- Desarrollar en forma teórica el método de Newton-Raphson para un sistema de n ecuaciones.
- Aplicar el método para resolver el sistema dado. Avanzar un paso partiendo de
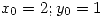
- Plantear una resolución de punto fijo para el sistema.
Ejercicio II
Se quiere realizar el siguiente cálculo:
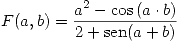
Se pide:
- Obtener el Cp y el Te
- Suponiendo que se trabaja con 8 dígitos de precisión, decir cuál debe ser la cota de los errores relativos de a y b para que el resultado tenga 6 dígitos correctos.
- Suponiendo que
 y que
y que  y los cálculos se realizane n una grilla con 3 dígitos de precisión. ¿Cuál es la cota del error relativo esperada a F?
y los cálculos se realizane n una grilla con 3 dígitos de precisión. ¿Cuál es la cota del error relativo esperada a F?
Ejercicio III
Dada la función 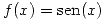 . Se pide:
. Se pide:
- Obtener el polinomio interpolador por el método de Newton en los puntos
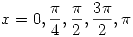 .
. - ¿Cuál debería ser el paso h si se desea realizar interpolación lineal con un error menor o igual al producido por el pòlinomio encontrado en el punto anterior?
- Plantee todas las consideraciones necesarias y el sistema de ecuaciones resultante (no resuelva) para obtener las splies cúbicas naturales para las abscisas planteadas en el punto 1.
- Implemente computacionalmente el método de Newton.
Resolución
Ejercicio I
Parte 1
Sea ![<tex>F(x_1,x_2,\ldots x_n)=\left[\begin{array}{c} f_1(x_1,x_2,\ldots x_n) \\ \vdots \\ f_n(x_1,x_2,\ldots x_n) \end{array} \right]</tex> <tex>F(x_1,x_2,\ldots x_n)=\left[\begin{array}{c} f_1(x_1,x_2,\ldots x_n) \\ \vdots \\ f_n(x_1,x_2,\ldots x_n) \end{array} \right]</tex>](lib/plugins/latex/images/cb726c4678d1054d52ee7852241f492de18d8044_0.png)
Si 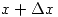 es la raíz de
es la raíz de 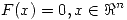
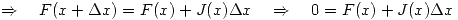

Puede pensarse un sistema iterativo: 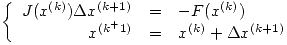 Partiendo de un
Partiendo de un 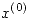 arbitrario y hasta que
arbitrario y hasta que  , donde
, donde 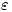 es la precisión que se desea obtener.
es la precisión que se desea obtener.
Parte 2
![<tex>F(x,y)=\left[\begin{array}{c} x^2+y^2-6 \\ x\cdot y-2 \end{array} \right]</tex> <tex>F(x,y)=\left[\begin{array}{c} x^2+y^2-6 \\ x\cdot y-2 \end{array} \right]</tex>](lib/plugins/latex/images/4a1a2262bfd1ff27071332630998325deb4a7acc_0.png)
Para hallar la raíz aploco el sistema iterativo de Newton-Rhapson, para lo que debo calcular ![<tex>J(x,y)=\left[\begin{array}{cc} 2x & 2y \\ y & x \end{array} \right]</tex> <tex>J(x,y)=\left[\begin{array}{cc} 2x & 2y \\ y & x \end{array} \right]</tex>](lib/plugins/latex/images/a9a66c716cc5f395c702c8f8f0a123a6de796102_0.png) .
.
![<tex>x^{(0)}=\left[\begin{array}{c} 2 \\ 1 \end{array} \right] \quad J(x^{(0)})=\left[\begin{array}{cc} 4 & 2 \\ 1 & 2 \end{array} \right] \quad \Rightarrow \quad \left[\begin{array}{cc} 4 & 2 \\ 1 & 2 \end{array} \right]\cdot \Delta x^{(1)}= \left[\begin{array}{c} 2 \\ 1 \end{array} \right]</tex> <tex>x^{(0)}=\left[\begin{array}{c} 2 \\ 1 \end{array} \right] \quad J(x^{(0)})=\left[\begin{array}{cc} 4 & 2 \\ 1 & 2 \end{array} \right] \quad \Rightarrow \quad \left[\begin{array}{cc} 4 & 2 \\ 1 & 2 \end{array} \right]\cdot \Delta x^{(1)}= \left[\begin{array}{c} 2 \\ 1 \end{array} \right]</tex>](lib/plugins/latex/images/8ba7c634c42e29887b0c20cbb8a6aac1218a4aa8_0.png)
Resolviendo este sistema se obtiene ![<tex>\Delta x^{(1)}= \left[\begin{array}{c} \displaystyle \frac{1}{3} \\ \displaystyle \frac{1}{3} \end{array} \right]</tex> <tex>\Delta x^{(1)}= \left[\begin{array}{c} \displaystyle \frac{1}{3} \\ \displaystyle \frac{1}{3} \end{array} \right]</tex>](lib/plugins/latex/images/cbf3d6fbbe38f34c1b586e4e96cb3417c153e2be_0.png) . Por lo tanto:
. Por lo tanto:
![<tex>x^{(1)}= \left[\begin{array}{c} \displaystyle \frac{7}{3} \\ \displaystyle \frac{4}{3} \end{array} \right]</tex> <tex>x^{(1)}= \left[\begin{array}{c} \displaystyle \frac{7}{3} \\ \displaystyle \frac{4}{3} \end{array} \right]</tex>](lib/plugins/latex/images/f90472f5869a9b230759f39ce03de7e6390471e8_0.png)
Parte 3
El sistema a resolver puede expresarse como 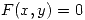 , entonces puedo plantear una solución de punto fijo
, entonces puedo plantear una solución de punto fijo 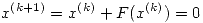 , es decir:
, es decir:
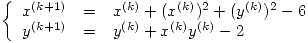
Entonces: ![<tex>\Phi(x,y)=\left[\begin{array}{c} x+x^2+y^2-6 \\ y+x\cdot y-2 \end{array}\right]</tex> <tex>\Phi(x,y)=\left[\begin{array}{c} x+x^2+y^2-6 \\ y+x\cdot y-2 \end{array}\right]</tex>](lib/plugins/latex/images/cf00b4e6658b7a86334ceb74fc7d3714ab62ac64_0.png)
y 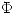 es la función de punto fijo tal que
es la función de punto fijo tal que 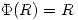 donde
donde 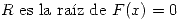 y
y 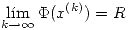 .
.
Ejercicio III
Parte 1
Interpolar por los puntos:
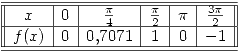
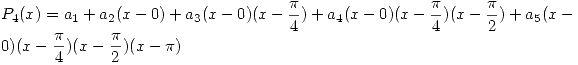
Tabla de diferencias divididas:

Entonces:
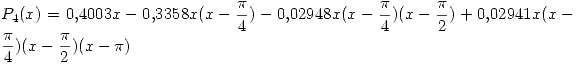
Parte 2
Primero debemos acotar el error de 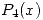
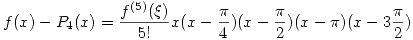
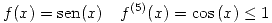
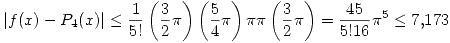
Para interpolación lineal en un intervalo de paso 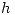
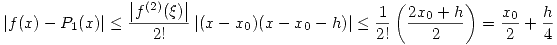
haciendo: 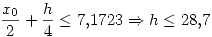
Un paso tan grande es inconsistente, pero esto surge de la acotación grosera de 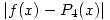 que fue realizada sin el debido análisis.
que fue realizada sin el debido análisis.
Parte 3
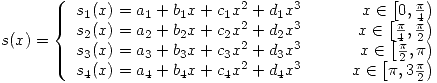
Planteo las ecuaciones de continuidad:
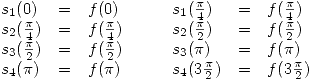
Y para las derivadas primeras:
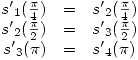
Y derivadas segundas:
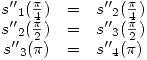
Y la condición de spline natural:
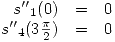
Parte 4
Realizar un algoritmo que obtenga los 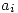 del polinomio interpolador de Newton en un vector N.
del polinomio interpolador de Newton en un vector N.
LEER X, Y, n
PARA i=1...n
A(i,1)=Y(i)
FIN PARA i
PARA j=2...n
PARA i=j..n
A(i,j)=(A(i,j-1)-A(i-1,j-1))/(X(i)-X(i-j+1))
FIN PARA i
FIN PARA j
PARA k=1...n
N(k)=A(k,k)
IMPRIMIR 'a_',k,'=',N(k)
FIN PARA k
FIN
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá o mándame un mail GK
