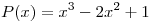Examen Parcial - 75.12. Análisis Numérico
Cátedra: Griggio
Fecha: Primera Oportunidad - Segundo Cuatrimestre 2007
Día: 31/10/2007
Tema: 1
Enunciado
Ejercicio I
Dado el siguiente sistema lineal 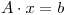 y utilizando una grilla numérica de punto flotante de 3 dígitos con redondeo simétrico. Se pide lo siguiente:
y utilizando una grilla numérica de punto flotante de 3 dígitos con redondeo simétrico. Se pide lo siguiente:
![<tex>\left[ \begin{array}{ccc}3.13 & 142 & 1 \\ 1.6 & 3.2 & 2 \\ 4.5 & 7.8 & 3 \end{array} \right]</tex> <tex>\left[ \begin{array}{ccc}3.13 & 142 & 1 \\ 1.6 & 3.2 & 2 \\ 4.5 & 7.8 & 3 \end{array} \right]</tex>](lib/plugins/latex/images/0c35eab778ddf869733b20e4b7aaae8267ce7d47_0.png)
![<tex>\left[ \begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \\ \end{array} \right]</tex> <tex>\left[ \begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \\ \end{array} \right]</tex>](lib/plugins/latex/images/0769e39243c5ab94307d7cd4855e61ac17a15229_0.png) =
=
![<tex>\left[ \begin{array}{c} 290 \\ 14 \\ 29.1 \\ \end{array} \right]</tex> <tex>\left[ \begin{array}{c} 290 \\ 14 \\ 29.1 \\ \end{array} \right]</tex>](lib/plugins/latex/images/7a72dff633fc0f00e548befa4c9403885a94a941_0.png)
- Hallar la solución del sistema mediante el método de Gauss sin pivoteo. Hallar también la factorización
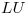 de la matriz
de la matriz  . (12 puntos)
. (12 puntos) - Utilizando la factorización hallada en el punto anterior, realizar un paso de refinamiento iterativo. (10 puntos)
- Hallar la solución mediante el método de Gauss con pivoteo parcial por intercambio de filas. (13 puntos)
- Compare las soluciones halladas en los tres puntos anteriores e indique qué método es más eficaz y porqué. La solución real del sistema es
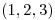 . También indique si puede utilizar los resultados de los primeros dos puntos para estimar
. También indique si puede utilizar los resultados de los primeros dos puntos para estimar 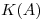 . ¿Está bien condicionado el sistema? (10 puntos)
. ¿Está bien condicionado el sistema? (10 puntos)
Ejercicio II
Dada la función 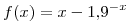 , se pide encontrar el cero de
, se pide encontrar el cero de 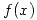 que se encuentra en el intervalo
que se encuentra en el intervalo ![<tex>[0;1]</tex> <tex>[0;1]</tex>](lib/plugins/latex/images/b4508b9928ddb137a742388e55ed5711cab7f26e_0.png) :
:
- Mediante la función de iteración de punto fijo
 . (15 puntos)
. (15 puntos) - Mediante el método de Newton-Raphson. (15 puntos)
En ambos casos efectúe los cálculos para llegar al punto fijo respectivo con un error absoluto menor que 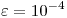 . Verifique si ambas funciones satisfacen las condiciones del Teorema del Punto Fijo. Calcule en ambos casos el orden de convergencia y la constante asintótica del error.
. Verifique si ambas funciones satisfacen las condiciones del Teorema del Punto Fijo. Calcule en ambos casos el orden de convergencia y la constante asintótica del error.
Ejercicio III
Dadas las siguientes 4 condiciones, se pide hallar el polinomio interpolante de menor grado que las satisface. (25 puntos)
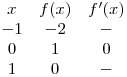
Resolución
Ejercicio I
Ejercicio II
Ejercicio III
La tabla de diferencias divididas por el método híbrido entre Newton y Hermite:

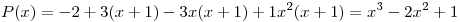
Verificamos que el polinomio verifique las condiciones:
Derivando obtenemos: 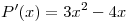
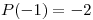
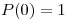
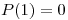
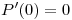
Como vemos, satisface las cuatro condiciones pedidas.
Nota: Como el polinomio interpolador es único, aunque se resuelva por otro método (por ejemplo, Lagrange) debemos obtener el mismo resultado.