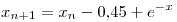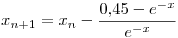Examen Parcial - 75.12. Análisis Numérico

Examen Parcial - 75.12. Análisis Numérico

Cátedra: Hernán Gonzalez
Fecha: Primera Oportunidad - Segundo Cuatrimestre 2006
Día: 27/10/2006

Enunciado

Ejercicio I

Se desea encontrar el cero de la función $<tex>f(x)= 0.45 - e^{-x}</tex>$
Para ello se proponen dos métodos iterativos:

$<tex>x_{n+1}=x_n - 0.45 + e^{-x}</tex>$
$<tex>x_{n+1}=x_n - \frac{0.45 - e^{-x}}{e^{-x}}</tex>$

Estudiar en cada caso las condiciones de convergencia
Estimar el orden de convergencia experimentalmente y compárelo con el valor teórico
Utilice el método que tenga mayor orden de convergencia para calcular el cero con una tolerancia para el error relativo menor del 1%

Ejercicio II

Sea 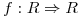$<tex>f: R \Rightarrow R</tex>$ tal que $<tex>f(\pm 3) = f( \pm 1) = 0 ; f(0) = 1 \ \mbox{y} \ |f^{(v)}(x)| < 1 \ \forall \ x \ \epsilon \ [-3,3]</tex>$

Halle un polinomio de grado 4 o menor que coincida con f en los 5 puntos dados
Estime el error que comete al reemplazar la función por el polinomio

Ejercicio III

Sea el siguiente sistema de ecuaciones lineales:
$<tex>\left\{ \begin{array}{l}x-10y-z = 4 \\4x+y-z = 13 \\2x-y+3z = 5 \\\end{array} \right.</tex>$

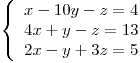
Resuelva si es posible el sistema planteado con un error menor del 0.05 utilizando el método de Jacobi

Ejercicio IV

Dada la siguiente expresión 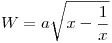$<tex>W = a \sqrt{x-\frac{1}{x}}</tex>$

Expresar mediante la gráfica de proceso el error relativo de W
si $<tex>a=\pi \ \mbox{y} \ x = 2.1</tex>$ exacto. ¿Cuántos dígitos debe tener la mantisa para que $<tex>|e_{rw}| \leq 0.05</tex>$ ?

Resolución

Discusión

Ayudanos con la resolución del parcial, cualquier colaboración será muy importante