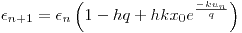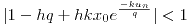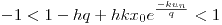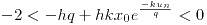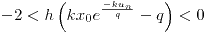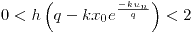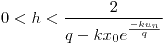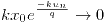Examen Final - 75.12. Análisis Numérico I - 28/07/08
Cátedra: Tarela
Fecha: ? Oportunidad - 1º Cuatrimestre 2008
Día: 28/07/2008
Enunciado
Problema 1
Para un población aislada, en la que se propaga una enfermedad contagiosa, el numero de personas 
que al tiempo 
se separa del resto por aislamiento se describe como: ![<tex>\frac{dz}{dt} = q \cdot[m-z-x_0 \cdot e^{\left(-\frac{k \cdot z}{q}\right)}]</tex>](lib/plugins/latex/images/d87fd4ff2098e73f831485b130be683695248f38_0.png "<tex>\frac{dz}{dt} = q \cdot[m-z-x_0 \cdot e^{\left(-\frac{k \cdot z}{q}\right)}]</tex>")
con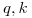 
constantes mayores que cero,
poblacion total,
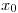cantidad de personas vulnerables y en días.
a) discretizar usando Euler explicito y analizar estabilidad del sistema
b) Para el caso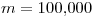 
, 
, 
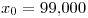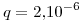y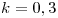 
encontrar el numero de individuos al cabo de 30 días.
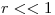de forma que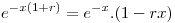 
Problema 2
Para la integral doble, hallar en forma exacta el error cometido al resolverla mediante cuadratura de Gauss con 2 puntos: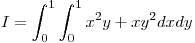 
Para ello determine los coeficientes y puntos de Gauss. Explica el resultado
Sugerencia: integre en una dirección y luego en otra.
Pregunta 1
Explique 3 métodos numéricos de distinto orden de convergencia para resolver una ecuación no lineal. Enumere ventajas y desventajas relativas entre ellos.
Pregunta 2
Explique la principal motivación que llevo al desarrollo de métodos multipaso para resolver una EDO.
Resolución
Punto I
![<tex>u_{n+1} = u_n + h q \left[ m - u_n - x_0 e^{ \frac{-k u_n}{q} } \right] </tex>](lib/plugins/latex/images/16a4d734f100a56cfb8494f6fd564a842b87ca2a_0.png "<tex>u_{n+1} = u_n + h q \left[ m - u_n - x_0 e^{ \frac{-k u_n}{q} } \right] </tex>")
![<tex>u_{n+1} + \epsilon_{n+1} = u_n + e_n + h q \left[ m - u_n - \epsilon_n - x_0 e^{ \frac{-k}{q}(u_n + \epsilon_n) } \right] </tex>](lib/plugins/latex/images/2cfaa7bc843050937a7f6901a794756af1d3e154_0.png "<tex>u_{n+1} + \epsilon_{n+1} = u_n + e_n + h q \left[ m - u_n - \epsilon_n - x_0 e^{ \frac{-k}{q}(u_n + \epsilon_n) } \right] </tex>")
![<tex>u_{n+1} + \epsilon_{n+1} = u_n + e_n + h q \left[ m - u_n - \epsilon_n - x_0 e^{\frac{-k u_n}{q}(1 + \frac{\epsilon_n}{u_n}) } \right] </tex>](lib/plugins/latex/images/19a8fe45937e747ded54aafefb7844bd40f64ad5_0.png "<tex>u_{n+1} + \epsilon_{n+1} = u_n + e_n + h q \left[ m - u_n - \epsilon_n - x_0 e^{\frac{-k u_n}{q}(1 + \frac{\epsilon_n}{u_n}) } \right] </tex>")
![<tex>u_{n+1} + \epsilon_{n+1} = u_n + e_n + h q \left[ m - u_n -\epsilon_n - x_0 e^{ \frac{-k u_n}{q} } (1 + \frac{\epsilon_n}{u_n}) \right] </tex>](lib/plugins/latex/images/37959273655995ce56ee0ac9a846ae0eca96b08d_0.png "<tex>u_{n+1} + \epsilon_{n+1} = u_n + e_n + h q \left[ m - u_n -\epsilon_n - x_0 e^{ \frac{-k u_n}{q} } (1 + \frac{\epsilon_n}{u_n}) \right] </tex>")
![<tex>u_{n+1} + \epsilon_{n+1} = u_n + hq \left[ m - u_n - x_0 e^{ \frac{-k u_n}{q} } \right] + \epsilon_n + h q \left[ -\epsilon_n + x_0 \frac{\epsilon_n k}{q} e^{ \frac{-k u_n}{q} } \right] </tex>](lib/plugins/latex/images/673eb5efc59a2a31cc96d170cb2bf0481576535d_0.png "<tex>u_{n+1} + \epsilon_{n+1} = u_n + hq \left[ m - u_n - x_0 e^{ \frac{-k u_n}{q} } \right] + \epsilon_n + h q \left[ -\epsilon_n + x_0 \frac{\epsilon_n k}{q} e^{ \frac{-k u_n}{q} } \right] </tex>")
