Examen Final - 75.12. Análisis Numérico I - 24/07/2008
Cátedra: Tarela
Fecha: ? Oportunidad - 1º Cuatrimestre 2008
Día: 24/07/2008
Enunciado
Problema 1
Se desea integrar numéricamente la ecuación de Van der Pol:
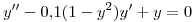a) Plantear las expresiones que surgen de aplicar el método de Runge Kutta de 4to orden
b) Avanzar la solución un paso de cálculo considerando k=0.2 para el caso en que y(0)=1, y´(0)=0
(ayuda: siendo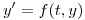 
y 
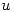la variable discreta asociada a 
:
)
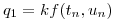
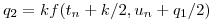
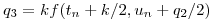
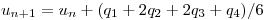Problema 2
a) Analizar si el siguiente método numérico para integrar PVI de primer orden es consistente e indicar cual es el orden de su error de discretización
![<tex>u_{n+1} = u_{n} + k/3[f(t_{n},u_{n}) + 2f(t_{n} + 3/4k,u_{n} + 3/4kf(t_{n},u_{n}))]</tex>](lib/plugins/latex/images/c7cd0518ffa163b7825f5607166dbae7acb514fc_0.png "<tex>u_{n+1} = u_{n} + k/3[f(t_{n},u_{n}) + 2f(t_{n} + 3/4k,u_{n} + 3/4kf(t_{n},u_{n}))]</tex>")
b) Aplicar el método anterior para calcular la solución del siguiente PVI en t=3 usando paso k=0.5
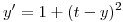con y(2) = 1 cuya solucion es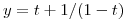 
c) Recalcular el método con k=1.0 y aplicar la extrapolación de Richardson para obtener un resultado más preciso que el obtenido en el punto anterior.
Pregunta 1
¿Cuál es el polinomio de mayor grado que puede ser integrado en forma exacta por los métodos de Rectángulo, Trapecio, Simpson y Gauss-Legendre de n puntos?. Justificar la respuesta.
Pregunta 2
¿Cuál método de interpolación conviene usar si luego se van a incorporar nuevos puntos de interpolación para aumentar el grado del polinomio interpolante?. Justificar la respuesta.
Resolución
