Examen Final - 75.12. Análisis Numérico I - 25/02/2008
Cátedra: Tarela
Fecha: 2º Cuatrimestre 2007
Día: 25/02/2008
Enunciado
Problema 1
La siguiente integral definida fue evaluada numéricamente utilizando el método de Simpson.
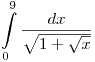
Obteniéndose para distintos tamaños de paso de cálculo 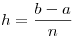 los resultados que se presentan en la siguiente tabla:
los resultados que se presentan en la siguiente tabla:
| n | S(h) |
|---|---|
| 4 | 5.45296 |
| 8 | 5.37796 |
| 16 | 5.34967 |
| 32 | 5.33923 |
Se pide:
a) Determinar el orden del error de truncamiento que presentan los resultados tabulados sabiendo que el valor exacto de la integral evaluada es 16/3. Justificar la metodología adoptada para efectuar esta determinación utilizando los conocimientos teóricos desarrollados en el curso.
b) Teniendo en cuenta el análisis efectuado en el punto anterior, aplicar extrapolación de Richardson para reducir el error de truncamiento de los resultados tabulados en aquellos casos en que sea posible hacerlo.
c) ¿Considera usted que el comportamiento observado es el esperado o piensa que existen discrepancias? Si esto ultimo fuera el caso, ¿encuentra usted alguna justificación de las discrepancias observadas?
Problema 2
Dado el siguiente PVI 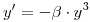 con
con 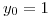 donde
donde 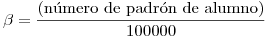
Se pide discretizarlo mediante el método de Euler usando un paso k constante y
a) analizar su estabilidad numérica y determinar kmáx de forma tal que esta última esté garantizada para todo k positivo menor que kmáx (Ayuda: analizar el comportamiento de la solución)
b) calcular la solución aproximada en T=1 tomando un h=0.5
c) calcular la solución aproximada en T=1 tomando un h=0.25
d) estimar el error de truncamiento del resultado obtenido en c) usando los resultados previamente calculados.
Pregunta 1
Los errores que afectan los resultados de un cálculo numérico pueden ser clasificados como: inherentes, de redondeo, o de discretización (también llamado de truncamiento). En el caso del refinamiento iterativo de la solución de sistemas lineales, ¿qué tipo de error se pretende reducir? Justifique su respuesta.
Pregunta 2
Explicar en qué consiste un problema de capa límite. ¿Cuál es el método que se recomienda para resolverlo? ¿Por qué?
Resolución
Punto 1
(a) Para determinar el orden del error de truncamiento comienzo planteando la siguiente ecuación: 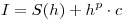 . Esto quiere decir que el valor exacto de la integral es igual al valor hallado por el método numérico más un término correspondiente al error de truncamiento que depende del el paso de calculo elevado a la p (siendo p el orden del error de truncamiento).
. Esto quiere decir que el valor exacto de la integral es igual al valor hallado por el método numérico más un término correspondiente al error de truncamiento que depende del el paso de calculo elevado a la p (siendo p el orden del error de truncamiento).
El valor exacto de la integral es dato y también se tiene tabulado el valor numérico calculado para distintos pasos de cálculo. Tomando los dos pasos más pequeños se plantea el siguiente sistema:
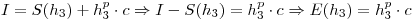
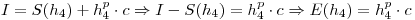
Dividiendo una ecuación con la otra queda:
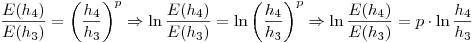
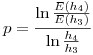

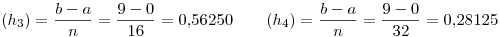
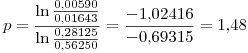
Procediendo de igual manera pero tomando los pasos de cálculo 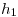 y
y 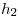 obtengo:
obtengo:

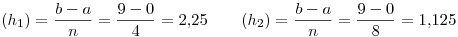
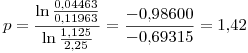
Promediando ambos resultados se obtiene un valor para el orden del error de truncamiento 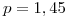 .
.
(b) Voy a aplicar la extrapolación a los resultados hallados con los pasos de cálculo 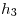 y
y 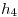 ; los más cercanos al resultado exacto. De la misa manera se puede realizar la extrapolación con los restantes datos de la tabla.
; los más cercanos al resultado exacto. De la misa manera se puede realizar la extrapolación con los restantes datos de la tabla.
Planteo la extrapolación de Richardson partiendo del siguiente sistema de ecuaciones:
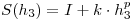
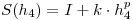
Restando la segunda con la primera:
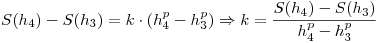
Reemplazando arriba en la primera ecuación:
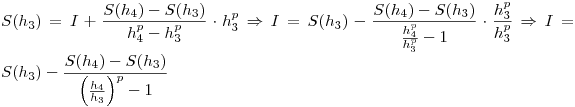
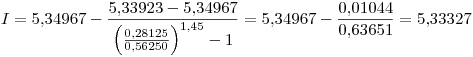
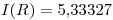
Vemos que al aplicar la extrapolación se obtiene un valor mucho más cercano al exacto.
(c ) El comportamiento observado no es el esperado ya que el método de Simpson tiene un error de truncamiento de orden 4, mayor al hallado experimentalmente. Esto se debe a que el integrando no cumple en  los requisitos de derivabilidad necesarios para tener un método de integración de cuarto orden. De hecho, ya no existe la derivada primera en
los requisitos de derivabilidad necesarios para tener un método de integración de cuarto orden. De hecho, ya no existe la derivada primera en  .
.
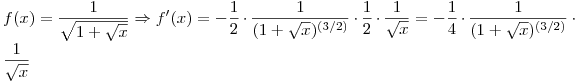
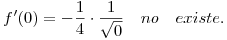
Punto 2
(a) Método de Euler: 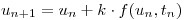
Discretizo mediante este método: 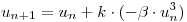
Planteo la estabilidad numérica:
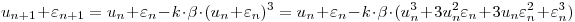
Desprecio los términos que contienen 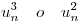 ya que al ser
ya que al ser 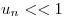 resulta ser
resulta ser 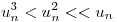 .
.
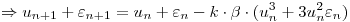
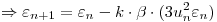
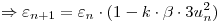
Para que el método sea estable se debe cumplir que: 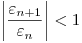
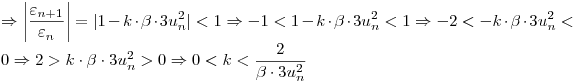
Como la función es positiva y decreciente (esto se ve en la expresión de la primera derivada que es negativa) se puede acotar el valor de k reemplazando en la expresión anterior a 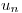 por
por 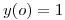 para obtener un valor de k máximo como se pide en el enunciado.
para obtener un valor de k máximo como se pide en el enunciado.
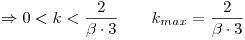
La estabilidad numérica queda garantizada para todo k positivo menor que el k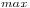 hallado.
hallado.
(b) Tomo 
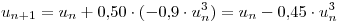
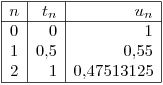
(c ) Tomo 
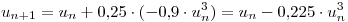
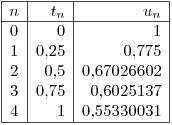
(d) Para estimar el error de truncamiento del resultado obtenido en c) usando los resultados previamente calculados puedo utilizar la extrapolación de Richardson para obtener un resultado más exacto y comparar a éste con el obtenido en c).
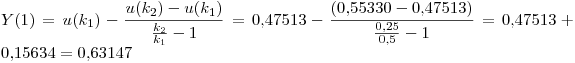
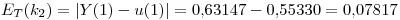
Pregunta 1
El refinamiento iterativo se aplica a métodos directos de resolución de sistemas de ecuaciones lineales. Estos métodos no presentan errores de truncamiento (a diferencia de los iterativos) pero presentan mayor cantidad de operaciones por lo que tienden a sufrir mayores errores de redondeo. El refinamiento iterativo busca disminuir este tipo de error.
Pregunta 2
Un problema de capa límite se presenta en los PVC en los que el factor que multiplica a 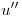 es mucho menor al que multiplica a
es mucho menor al que multiplica a 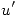 :
: 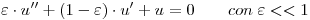
En este tipo de problemas, la solución cambia rápidamente en una franja muy estrecha del dominio y admite un paso de cálculo muy pequeño al resolverlo mediante un método directo. Si se toma un paso mayor al estipulado por las condiciones de estabilidad, la solución numérica dista notablemente de la solución analítica presentando oscilaciones.
Una forma de mejorar la solución numérica es descentrar la derivada primera (upwinding o downwinding). De esta manera se pierde el orden 2 (lo que implica un error de truncamiento) aunque se disminuye notablemente la oscilación del método.
