Examen Final - 75.12. Análisis Numérico I - 18/02/08

Cátedra: Tarela
Fecha: ? Oportunidad - 2º Cuatrimestre 2007
Día: 18/02/2008

Dada la siguiente integral doble:

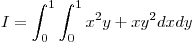
a) Hallar en forma exacta el error cometido al resolverla mediante cuadratura de Gauss con 2 puntos. Sugerencia: integre numéricamente en una dirección, y luego en la otra.
b) Con las bases teóricas del curso, explicar el resultado.
Datos: puntos de Gauss = 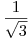, 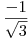; Coeficientes de cuadratura = 1,1.

Se tiene el siguiente problema diferencial:

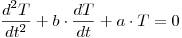
a) Elegir un método adecuado de discretización de orden 2, de entre los siguientes, justificando su respuesta:
1) Euler, 2) Runge-Kutta 2, 3) Diferencias Finitas, 4) Upwinding, 5) Newmark.
b) Discretizar el problema con el método seleccionado usando un paso h=1/3.
c) Hallar la solución numérica para el caso a=1, b=1.

Mostrar que el método del punto fijo para hallar la única raíz de una ecuación no lineal dentro de un intervalo determinado, es de orden 1.

Indique justificadamente cuál es la principal ventaja de un método explicito para resolver una EDO. ¿Cual es la principal ventaja de un método explicito?