Tabla de Contenidos
Exámen Final - 75.12 Análisis Numérico I
Cátedra: Cavaliere - Tarela
Fecha: Segundo cuatrimestre, 2013
Día: 18/12/2013
Enunciado
Resolución
Problema 1
Parte a)
Se plantea el cambio de siguiente cambio de variable:
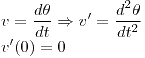
Aplicamos este cambio a la ecucación original, quedando el sistema:
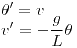
Antes de aplicar Euler como se pide, hay que recordar que
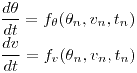
Dicho esto, discretizamos las funciones aplicando Euler:
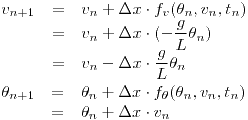
En donde, sin olvidarnos las condiciones iniciales, se cumple que
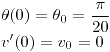
Parte b)
Si aplicamos un paso de 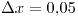 podemos tener una decente aproximación en el séptimo paso.
El valor de la derivada en dicho paso es
podemos tener una decente aproximación en el séptimo paso.
El valor de la derivada en dicho paso es 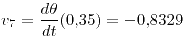
NOTA:
Con un paso  la derivada se conoce en el paso catorce y da
la derivada se conoce en el paso catorce y da 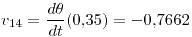
La solución analítica del problema es 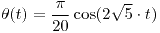
y la derivada evaluada en 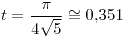 da
da 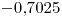
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported

