Examen Final - 75.12. Análisis Numérico I - 15/08/07
Cátedra: Daniel Griggio
Fecha: Quinta fecha - (1º Cuatrimestre) 2007
Día: 15/08/2007
Enunciado
Punto 1
Para la siguiente ecuación diferencial: 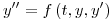 , y(0) = y0, y’(0) = u0, el método de Nystrom la discretiza directamente (sin pasar por un sistema de ecuaciones de primer orden) según:
, y(0) = y0, y’(0) = u0, el método de Nystrom la discretiza directamente (sin pasar por un sistema de ecuaciones de primer orden) según: 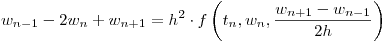 , donde la función f se refiere a la función de la ecuación original.
, donde la función f se refiere a la función de la ecuación original.
- Aplicar el esquema a la ecuación
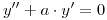 , y(0) = y’(0) = 1. Demostrar que resulta una ecuación en diferencias explícita con tres niveles de tiempo.
, y(0) = y’(0) = 1. Demostrar que resulta una ecuación en diferencias explícita con tres niveles de tiempo. - Analizar la estabilidad del esquema.
Punto 2
Para la siguiente integral: 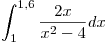
- Aproximarla por el método de los trapecios compuesto, utilizando h = 0,1.
- Aproximarla por Gauss-Legendre de cuatro puntos.
- Comparar con el valor exacto de la integral.
Datos: raíces del polinomio de Legendre y coeficientes:
| xi | Ci |
|---|---|
| ±0,861136 | 0,347855 |
| ±0,339981 | 0,652145 |
Resolución
Punto I
a) Despejando de la ecuación dada resulta  .
.
Reemplazando en la expresión del método de Nystrom (y reemplazando  por
por 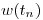 ):
):
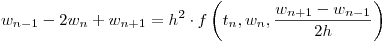 resulta en este caso:
resulta en este caso:
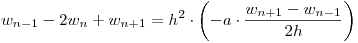
Despejando  se obtiene:
se obtiene: 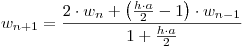 Se observa en esta expresión que se puede despejar
Se observa en esta expresión que se puede despejar  , de forma que resulta un método explícito. Además, en la expresión aparecen
, de forma que resulta un método explícito. Además, en la expresión aparecen  ,
,  y
y 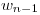 , es decir, los valores de w para los instantes
, es decir, los valores de w para los instantes 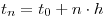 ,
, 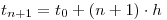 y
y 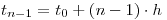 . Así se demuestra que en la ecuación en diferencias resultante intervienen tres niveles de tiempo.
. Así se demuestra que en la ecuación en diferencias resultante intervienen tres niveles de tiempo.
b) Planteando perturbaciones para cada valor y reemplazando en la expresión resulta:
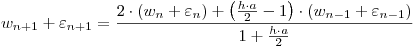 .
.
Como la ecuación es lineal y no interviene t, la ecuación de perturbación resulta:
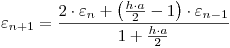
De forma de eliminar el tercer nivel de tiempo y llevarlo a sólo dos se realiza una sustitución 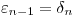 , de forma que
, de forma que 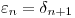 , resultando el sistema:
, resultando el sistema:
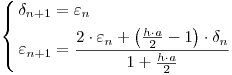
Modificando un poco la expresión:
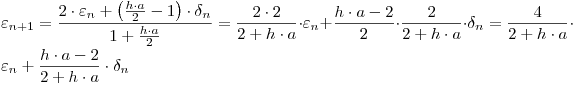
Matricialmente: ![<tex>\left[ {\begin{array}{*{20}c} {\varepsilon _{n + 1} } \\ {\delta _{n + 1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{4}{{2 + h \cdot a}}} & {\frac{{h \cdot a - 2}}{{2 + h \cdot a}}} \\ 1 & 0 \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {\varepsilon _n } \\ {\delta _n } \\ \end{array} } \right]</tex> <tex>\left[ {\begin{array}{*{20}c} {\varepsilon _{n + 1} } \\ {\delta _{n + 1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{4}{{2 + h \cdot a}}} & {\frac{{h \cdot a - 2}}{{2 + h \cdot a}}} \\ 1 & 0 \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {\varepsilon _n } \\ {\delta _n } \\ \end{array} } \right]</tex>](lib/plugins/latex/images/5a65e1f577cdebafac5723711c449b945745ea30_0.png)
Se necesita el radio espectral de la matriz de perturbaciones, para lo cual se calculan los autovalores:
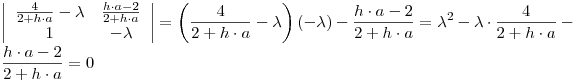
![<tex>\lambda _{1,2} = \frac{{\frac{4}{{2 + h \cdot a}} \pm \sqrt {\frac{{4^2 }}{{\left( {2 + h \cdot a} \right)^2 }} + 4 \cdot 1 \cdot \frac{{h \cdot a - 2}}{{2 + h \cdot a}}} }}{2} = \frac{1}{2} \cdot \left[ {\frac{4}{{2 + h \cdot a}} \pm \sqrt {\frac{{4^2 + 4 \cdot \left( {h \cdot a - 2} \right) \cdot \left( {2 + h \cdot a} \right)}}{{\left( {2 + h \cdot a} \right)^2 }}} } \right]</tex> <tex>\lambda _{1,2} = \frac{{\frac{4}{{2 + h \cdot a}} \pm \sqrt {\frac{{4^2 }}{{\left( {2 + h \cdot a} \right)^2 }} + 4 \cdot 1 \cdot \frac{{h \cdot a - 2}}{{2 + h \cdot a}}} }}{2} = \frac{1}{2} \cdot \left[ {\frac{4}{{2 + h \cdot a}} \pm \sqrt {\frac{{4^2 + 4 \cdot \left( {h \cdot a - 2} \right) \cdot \left( {2 + h \cdot a} \right)}}{{\left( {2 + h \cdot a} \right)^2 }}} } \right]</tex>](lib/plugins/latex/images/f2d6a88f62a903e50a8b184b9f0659c39d319086_0.png)
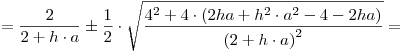
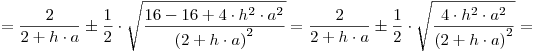
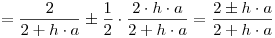

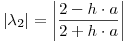
Para 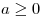 es estable debil y para
es estable debil y para 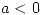 es inestable.
es inestable.
Punto II
a) Para la fórmula de trapecios resulta:
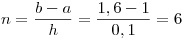 .
.
Usando la expresión de trapecios compuesto:
![<tex>T\left( h \right) = \frac{h}{2} \cdot \left[ {f\left( {x_0 } \right) + 2 \cdot \sum\limits_{i = 1}^{n - 1} {f\left( {x_i } \right)} + f\left( {x_n } \right)} \right]</tex> <tex>T\left( h \right) = \frac{h}{2} \cdot \left[ {f\left( {x_0 } \right) + 2 \cdot \sum\limits_{i = 1}^{n - 1} {f\left( {x_i } \right)} + f\left( {x_n } \right)} \right]</tex>](lib/plugins/latex/images/e63dd3699db13b6576b175b83f5d797121cfd485_0.png)
con 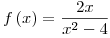 resulta:
resulta:
![<tex>T\left( {0,1} \right) = \frac{{0,1}}{2}\left[ { - 0,66667 + 2 \cdot \left( { - 0,78853 - 0,9375 - 1,12554 - 1,37255 - 1,71429} \right) - 2,2222} \right]</tex> <tex>T\left( {0,1} \right) = \frac{{0,1}}{2}\left[ { - 0,66667 + 2 \cdot \left( { - 0,78853 - 0,9375 - 1,12554 - 1,37255 - 1,71429} \right) - 2,2222} \right]</tex>](lib/plugins/latex/images/b42a63f01f242a01cf9f730dd359f3739c357779_0.png)
T(0,1) = – 0,73829
b) Según Gauss-Legendre: ![<tex>\int_{ - 1}^1 {f\left( x \right)dx} \simeq \sum\limits_{i = 1}^n {\left[ {C_i \cdot f\left( {x_i } \right)} \right]} </tex> <tex>\int_{ - 1}^1 {f\left( x \right)dx} \simeq \sum\limits_{i = 1}^n {\left[ {C_i \cdot f\left( {x_i } \right)} \right]} </tex>](lib/plugins/latex/images/08b30fbb38b89910bdbd1f4fb645c318d48fe677_0.png)
Se debe hacer un cambio de variables para ajustar el intervalo de integración.
Se cumple que 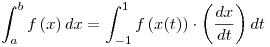 usando
usando 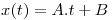 .
Planteando las condiciones
.
Planteando las condiciones 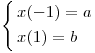 se obtiene la solución
se obtiene la solución 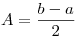 y
y 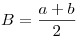 , con
, con 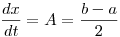 .
.
∴![<tex>\int_a^b {f\left( x \right)dx} = \frac{{b - a}}{2}\int_{ - 1}^1 {f\left( t \right)dt} \simeq \frac{{b - a}}{2}\sum\limits_{i = 1}^n {\left[ {C_i \cdot f\left( {x(t_i )} \right)} \right]}</tex> <tex>\int_a^b {f\left( x \right)dx} = \frac{{b - a}}{2}\int_{ - 1}^1 {f\left( t \right)dt} \simeq \frac{{b - a}}{2}\sum\limits_{i = 1}^n {\left[ {C_i \cdot f\left( {x(t_i )} \right)} \right]}</tex>](lib/plugins/latex/images/3ae3845e8d01a852d5dbe06e6a8f09561887d192_0.png)
Finalmente, con 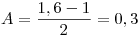 y
y 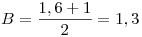 resulta:
resulta:
![<tex>\left[ { \ldots + 0,652145 \cdot f\left( { - 0,3 \cdot 0,339981 + 1,3} \right) + 0,652145 \cdot f\left( {0,3 \cdot 0,339981 + 1,3} \right) + \ldots } \right]</tex> <tex>\left[ { \ldots + 0,652145 \cdot f\left( { - 0,3 \cdot 0,339981 + 1,3} \right) + 0,652145 \cdot f\left( {0,3 \cdot 0,339981 + 1,3} \right) + \ldots } \right]</tex>](lib/plugins/latex/images/85cb7434be1eee08a1c18f4e3ccffae537d57ac8_0.png)
![<tex>\left[ { \ldots + 0,347855 \cdot f\left( {0,3 \cdot 0,861136 + 1,3} \right)} \right]</tex> <tex>\left[ { \ldots + 0,347855 \cdot f\left( {0,3 \cdot 0,861136 + 1,3} \right)} \right]</tex>](lib/plugins/latex/images/fa1b9a5358e9b8d9064517d15c220fc1a4723dcb_0.png)
![<tex>\int_1^{1,6} {\frac{{2x}}{{x^2 - 4}}dx} \simeq 0,3 \cdot \left[ {0,347855 \cdot f\left( {1,0416592} \right) + \ldots } \right]</tex> <tex>\int_1^{1,6} {\frac{{2x}}{{x^2 - 4}}dx} \simeq 0,3 \cdot \left[ {0,347855 \cdot f\left( {1,0416592} \right) + \ldots } \right]</tex>](lib/plugins/latex/images/f625a2c4dc95c7d32a66e298ec73ca0726c190af_0.png)
![<tex>\left[ { \ldots + 0,652145 \cdot f\left( {1,1980057} \right) + 0,652145 \cdot f\left( {1,4019943} \right) + \ldots } \right]</tex> <tex>\left[ { \ldots + 0,652145 \cdot f\left( {1,1980057} \right) + 0,652145 \cdot f\left( {1,4019943} \right) + \ldots } \right]</tex>](lib/plugins/latex/images/29892feccb09e12ad1674176128a1b075051ac2c_0.png)
![<tex>\left[ { \ldots + 0,347855 \cdot f\left( {1,5583408} \right)} \right]</tex> <tex>\left[ { \ldots + 0,347855 \cdot f\left( {1,5583408} \right)} \right]</tex>](lib/plugins/latex/images/6b5ecda06f4f9994ea9e2ae4efd99a5dac274b4b_0.png)
![<tex>\int_1^{1,6} {\frac{{2x}}{{x^2 - 4}}dx} \simeq 0,3 \cdot \left[ {0,347855 \cdot \left( { - 0,7147022} \right) + 0,652145 \cdot \left( { - 0,934196777} \right) + \ldots } \right]</tex> <tex>\int_1^{1,6} {\frac{{2x}}{{x^2 - 4}}dx} \simeq 0,3 \cdot \left[ {0,347855 \cdot \left( { - 0,7147022} \right) + 0,652145 \cdot \left( { - 0,934196777} \right) + \ldots } \right]</tex>](lib/plugins/latex/images/536db30356362d568f0adbb5280844b07bc82a78_0.png)
![<tex>\left[ { \ldots + 0,652145 \cdot \left( { - 1,378279633} \right) + 0,347855 \cdot \left( { - 1,983159366} \right)} \right]</tex> <tex>\left[ { \ldots + 0,652145 \cdot \left( { - 1,378279633} \right) + 0,347855 \cdot \left( { - 1,983159366} \right)} \right]</tex>](lib/plugins/latex/images/1206fb737748cbcd82c8ed5315fd66e1826a822c_0.png)
G = –0,73396
c) En forma exacta:
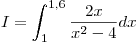 se resuelve realizando la sustitución
se resuelve realizando la sustitución  , de forma que
, de forma que
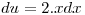 . Sustituyendo los límites de integración:
. Sustituyendo los límites de integración: 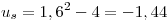 y
y
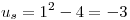 , resulta:
, resulta:
![<tex>I = \int_1^{1,6} {\frac{{2x}}{{x^2 - 4}}dx} = \int_{ - 3}^{ - 1,44} {\frac{1}{u}du} = \left. {\left[ {\ln \left| u \right|} \right]} \right|_{ - 3}^{ - 1,44} = \ln 1,44 - \ln 3 = \ln \frac{{12}}{{25}}</tex> <tex>I = \int_1^{1,6} {\frac{{2x}}{{x^2 - 4}}dx} = \int_{ - 3}^{ - 1,44} {\frac{1}{u}du} = \left. {\left[ {\ln \left| u \right|} \right]} \right|_{ - 3}^{ - 1,44} = \ln 1,44 - \ln 3 = \ln \frac{{12}}{{25}}</tex>](lib/plugins/latex/images/069d53d8ff48bdb5902be65937095650c3254bb2_0.png)
Resulta: I ≈ -0,7339691750
