Tabla de Contenidos
Examen Final - 75.12. Analisis Numérico I
Cátedra: Griggio-Navarro
Fecha: Cuarta Oportunidad - Primer Cuatrimestre 2007
Día: 10/08/2007
Esta página está incompleta; podés ayudar completando el material.
Enunciado
Punto I
Estudiar mediante perturbaciones la estabilidad del problema, discretizando con el método dado.
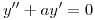 con
con 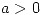 ,
, 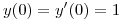
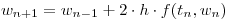
Punto II
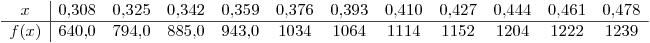
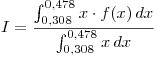
Dada la tabla estimar el valor de 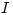 mediante: Trapecios, Simpson y Romberg.
mediante: Trapecios, Simpson y Romberg.
Resolución
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
