Examen Final - 75.12. Analisis Numérico I - 01/08/2007
Cátedra: Griggio-Navarro / 3
Fecha: Tercera Oportunidad - Primer Cuatrimestre 2007
Día: 01/08/2007
Enunciado
Punto I
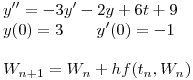
Parte A
Transformar la ecuación en un sistema de ecuaciones diferenciales de primer orden.
Parte B
Discretizar las ecuaciones obtenidas en la Parte A mediante el método de Euler convenientemente generalizado.
Parte C
Estudiar la estabilidad del sistema.
Punto II
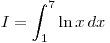
Parte A
Evaluar I usando el método de Simpson compuesto con un error menor a 0,005.
Parte B
Calcular el valor exacto de I y comparar con el resultado de la Parte A y verificar que el error es menor a 0,005.
Punto III
Se desea interpolar con spline cúbica natural una función con 4 nodos. Explicar cuáles son las incógnitas y ecuaciones que completan el problema.
Resolución
Punto II
Parte A
La fórmula del error de discretización para el método es: 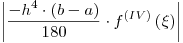 .
.
Como 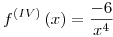 , resulta
, resulta 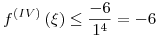 ya que 1 ≤ ξ ≤ 7.
ya que 1 ≤ ξ ≤ 7.
Pidiendo que 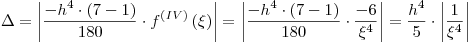 resulte
resulte 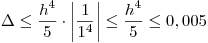 y despreciando los errores de redondeo frente a los de truncamiento se puede despejar el paso h, que resulta h≤0,3976353643.
y despreciando los errores de redondeo frente a los de truncamiento se puede despejar el paso h, que resulta h≤0,3976353643.
Usando paso h=0,3 es 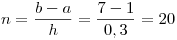 .
.
Calculando según la fórmula de Simpson compuesto ![<tex>I \approx \frac{h}{3}\left[ {f\left( {x_0 } \right) + 4 \cdot \sum\limits_{k = 0}^{\frac{n}{2} - 1} {f\left( {x_{2k + 1} } \right)} + 2 \cdot \sum\limits_{k = 1}^{\frac{n}{2} - 1} {f\left( {x_{2k} } \right)} + f\left( {x_n } \right)} \right]</tex> <tex>I \approx \frac{h}{3}\left[ {f\left( {x_0 } \right) + 4 \cdot \sum\limits_{k = 0}^{\frac{n}{2} - 1} {f\left( {x_{2k + 1} } \right)} + 2 \cdot \sum\limits_{k = 1}^{\frac{n}{2} - 1} {f\left( {x_{2k} } \right)} + f\left( {x_n } \right)} \right]</tex>](lib/plugins/latex/images/68136e3eb760601ec61b4636837dc42b3f6be6d6_0.png) , donde
, donde 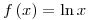 resulta
resulta 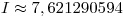 .
.
Parte B
En forma exacta es: ![<tex> I = \int_1^7 {\ln x\,dx} = \left. {\left[ {x\ln x - x} \right]} \right|_1^7 = 7 \cdot \ln 7 - 6 = {\rm{7}}{\rm{,621371043}}</tex> <tex> I = \int_1^7 {\ln x\,dx} = \left. {\left[ {x\ln x - x} \right]} \right|_1^7 = 7 \cdot \ln 7 - 6 = {\rm{7}}{\rm{,621371043}}</tex>](lib/plugins/latex/images/dbc03ff24a1be3b80e93a8e8681c9d0b1566a1eb_0.png) .
.
Se comprueba que resulta una diferencia recién en el 4º dígito decimal.
