Examen Final - 75.12. Analisis Numérico I
- Enunciado
  - Punto I
  - Punto II
- Resolución
- Discusión

Examen Final - 75.12. Analisis Numérico I

Cátedra: Griggio-Navarro
Fecha: Segunda Oportunidad - Primer Cuatrimestre 2007
Día: 25/07/2007

Esta página está incompleta; podés ayudar completando el material.

Enunciado

Punto I

Dada la siguiente tabla diga porqué no le sirve para estimar 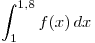$<tex>\int_{1}^{1.8} f(x) \, dx</tex>$ mediante Romberg:

$<tex>\begin{array}{c|cccccccc}x & 1.0 & 1.1 & 1.2 & 1.3 & 1.4 & 1.5 & 1.7 & 1.8 \\\hlinef(x) & 1.543 & 1.669 & 1.811 & 1.971 & 2.151 & 2.352 & 2.828 & 3.107 \end{array}</tex>$

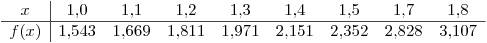
Corrija la tabla de manera sencilla y calcule la integral mediante Romberg.
Estime la integral mediante Simpson compuesto y calcule una cota del error de truncamiento sabiendo que $<tex>\vert{f^{IV}(x)} \vert <= 3.2</tex>$ $<tex>\forall x \in (1 ; 1.8)</tex>$

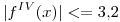
Punto II

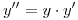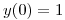Dada la ecuación diferencial de segundo orden: $<tex>y'' = y \cdot y'</tex>$ con $<tex>y(0) = 1</tex>$ , $<tex>y'(0) = 1</tex>$

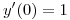
Escribir el sistema de ecuaciones diferenciales (SED) de primer orden equivalente.
Discretizar el SED aplicando el siguiente esquema predictor-corrector:
$<tex>w_{n+1} = w_{n} + h \cdot f(t_{n},w_{n})</tex>$
$<tex>w_{n+1} = w_{n} + \frac{h}{2} \cdot ( f(t_{n},w_{n}) + f(t_{n+1},w_{n+1}) )</tex>$
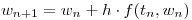
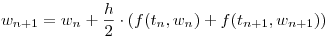
Estimar $<tex>y(0.3)</tex>$ usando $<tex>h = 0.1</tex>$ . Corregir en cada paso una vez.

Resolución

Discusión

Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.