Examen Final - 75.12. Analisis Numérico I
Cátedra: Griggio-Navarro
Fecha: Primera Oportunidad - Primer Cuatrimestre 2007
Día: 18/07/2007
Enunciado
Punto I
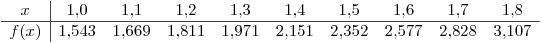
- Estimar
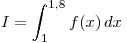 mediante la fórmula de trapecios con
mediante la fórmula de trapecios con 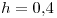 ,
, 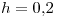 ,
,  .
. - La función tabulada es
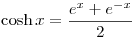 . Cuáles son los errores de
. Cuáles son los errores de 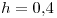 ,
, 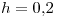 ,
,  . Comparar los errores dividiendo previamente por
. Comparar los errores dividiendo previamente por 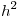 .
.
Punto II
Dada la ecuación diferencial de segundo orden:
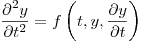 con
con  ,
, 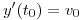
- Escribir el sistema de ecuaciones diferenciales (SED) de primer orden equivalente.
- Discretizar el SED aplicando el siguiente esquema predictor-corrector, generalizado convenientemente:
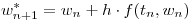
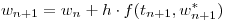
- Escribir el algoritmo que implemente lo obtenido en el punto anterior.
- Plantear la discretización obtenida anteriormente para el siguiente problema y estimar
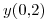 usando
usando  :
:
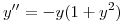 con
con 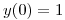 ,
, 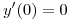
Resolución
Punto I
Fórmula de Trapecios Compuesto:
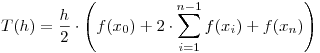
Pasamos a calcular en particular para 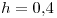 ,
, 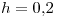 ,
,  .
.
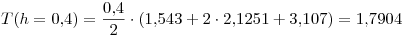
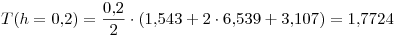
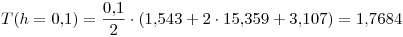
El error de la fórmula de trapecios compuesto es:
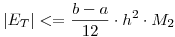
Lo que falta para poder hacer las comparaciones es una cota para la derivada segunda: 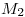
Derivamos dos veces la función: 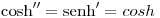
En particular la cota de la derivada segunda es la cota de la función en el intervalo, que se puede ver que es el valor máximo es el último valor de la tabla. Entonces 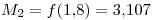 y lo reemplazamos en la fórmula del error:
y lo reemplazamos en la fórmula del error:
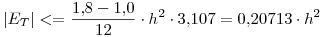
El error de trapecios depende del cuadrado del paso 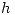 , pero al dividir por esta expresión, obtenemos la misma relación para todo
, pero al dividir por esta expresión, obtenemos la misma relación para todo 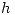 . Luego, si dividimos por
. Luego, si dividimos por 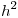 nos queda:
nos queda:
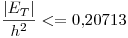
En particular, los errores para los pasos calculados son:
Para  ,
, 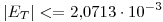
Para 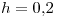 ,
, 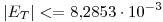
Para 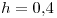 ,
, 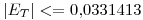
Como dato adicional, el valor real de la integral es: 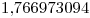 .
.
