Examen Final - 75.12. Análisis Numérico
Cátedra: Morelli
Fecha: Cuarta Oportunidad - Primer Cuatrimestre 2006
Día: 04/08/2006
Enunciado
Teoría
Deducir el error de truncamiento al calcular 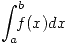 por la regla del rectángulo.
por la regla del rectángulo.
Diagrama de flujo
Escribir un diagrama de flujo para hallar la raíz de 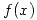 en
en ![<tex>[a,b]</tex> <tex>[a,b]</tex>](lib/plugins/latex/images/d8b00ad439a06f5f89f6503e870c04a5fe593bbc_0.png) ,
, 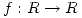 continua en
continua en ![<tex>[a,b]</tex> <tex>[a,b]</tex>](lib/plugins/latex/images/d8b00ad439a06f5f89f6503e870c04a5fe593bbc_0.png) con el método de Regula-Falsi. ¿Qué orden de convergencia tiene la sucesión generada? ¿Cuántas funciones evalúa en cada iteración?
con el método de Regula-Falsi. ¿Qué orden de convergencia tiene la sucesión generada? ¿Cuántas funciones evalúa en cada iteración?
Ejercicio 1
Estudiar medianto grafos la propagación del error, y decidir cuál de los siguientes métodos es conveniente:
- Clásico
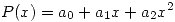
- Horner
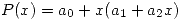
Ejercicio 2
Sea la siguiente ecuación diferencial con valores iniciales
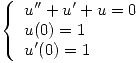
Transformarla en un sistema de ecuaciones diferenciales de Primer Orden
Decidir si las siguientes afirmaciones son Verdaderas o Falsas:
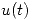 es creciente en
es creciente en 
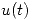 es decreciente en
es decreciente en 
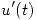 es creciente en
es creciente en 
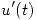 es decreciente en
es decreciente en 
- Calcular
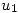 y
y 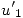 con
con 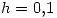 con los siguientes métodos:
con los siguientes métodos:- Euler explícito
- Runge-Kutta de orden 2, cuya función incremento aproximado para una sola variable es
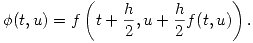
- Calcular
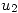 y
y 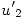 con el método de Adams-Bashforth de orden 2, es decir,
con el método de Adams-Bashforth de orden 2, es decir, 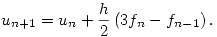
¿Qué ventajas y desventajas tienen los métodos multipasos frente a los métodos de un paso?
¿Qué orden debe tener el método de un paso para calcular el valor de arranque?
Resolución
Teoría
Si se particiona el intervalo en  partes iguales
partes iguales 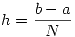

Entonces se aproxima la integral: 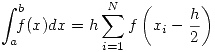
Entonces el error en cada intervalo es:
![<tex>DI_i=\int_{x_{i-1}}^{x_i} \!\!\!\! [ f(x) - f\left( x_i -\frac{h}{2} \right) ] dx</tex> <tex>DI_i=\int_{x_{i-1}}^{x_i} \!\!\!\! [ f(x) - f\left( x_i -\frac{h}{2} \right) ] dx</tex>](lib/plugins/latex/images/88beb3b470233a27b50397e82c62f01103770a8b_0.png)
Si desarrollo el polinomio de Taylor alrededor de 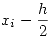 obtengo:
obtengo:
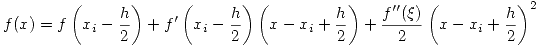
Si calculo la primera integral:
![<tex>\int_{x_{i-1}}^{x_i} \!\!\!\! f'\left( x_i -\frac{h}{2} \right) \left( x-x_i +\frac{h}{2} \right) dx = f'\left( x_i -\frac{h}{2} \right) \left[ \left. \frac{\left( x-x_i +\frac{h}{2} \right)^2}{2} \right|_{x_{i-1}}^{x_i} \right]=f'\left( x_i -\frac{h}{2} \right) \left[ \frac{h^2}{8}-\frac{h^2}{8} \right] =0 </tex> <tex>\int_{x_{i-1}}^{x_i} \!\!\!\! f'\left( x_i -\frac{h}{2} \right) \left( x-x_i +\frac{h}{2} \right) dx = f'\left( x_i -\frac{h}{2} \right) \left[ \left. \frac{\left( x-x_i +\frac{h}{2} \right)^2}{2} \right|_{x_{i-1}}^{x_i} \right]=f'\left( x_i -\frac{h}{2} \right) \left[ \frac{h^2}{8}-\frac{h^2}{8} \right] =0 </tex>](lib/plugins/latex/images/80c385b49f7692dd02225663e7b20e05e0e8cbf3_0.png)
La segunda integral es:
![<tex>\int_{x_{i-1}}^{x_i} \!\!\!\! \frac{f''(\xi)}{2} \left( x-x_i +\frac{h}{2} \right)^2 dx = \frac{f''(\xi)}{2} \left[ \left. \frac{\left( x-x_i +\frac{h}{2} \right)^3}{3} \right|_{x_{i-1}}^{x_i} \right] = \frac{f''(\xi)h^3}{24}</tex> <tex>\int_{x_{i-1}}^{x_i} \!\!\!\! \frac{f''(\xi)}{2} \left( x-x_i +\frac{h}{2} \right)^2 dx = \frac{f''(\xi)}{2} \left[ \left. \frac{\left( x-x_i +\frac{h}{2} \right)^3}{3} \right|_{x_{i-1}}^{x_i} \right] = \frac{f''(\xi)h^3}{24}</tex>](lib/plugins/latex/images/59c0bf4416c292b40566f5da3052eacd1cb4a2df_0.png)
Entonces: 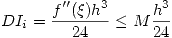 siendo
siendo ![<tex> M \geq \sup_{x\in [a,b]} f''(x)</tex> <tex> M \geq \sup_{x\in [a,b]} f''(x)</tex>](lib/plugins/latex/images/5f4883f7f19023b85d98a27d0c818dbd825ce50a_0.png)
El error de truncamiento es entonces:
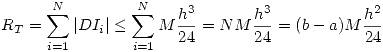
Diagrama de Flujo
Para no hacer el diagrama de flujo lo escribo en pseudo-código:
LEER a,b,tol
FA=f(a)
FB=f(b)
REPETIR
c=a-FA*(b-a)/(FB-FA)
FC=f(c)
SI FC*FA<0
HACER
b=c
FB=FC
SINO HACER
a=c
FA=FC
FIN SI
HASTA |FC|<tol
IMPRIMIR c
FIN
La sucesión generada tiene orden 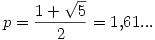
Así como se ha escrito evalúa una sóla función en cada iteración
FC=f(c)
Por lo que la eficiencia del método es igual al orden.
Ejercicio 1
Ejercicio 2
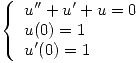
Haciendo  la ecuación se transforma en el sistema:
la ecuación se transforma en el sistema:
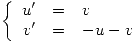
Con las condiciones iniciales:
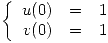
Para escribir en forma matricial defino: ![<tex>\vec{u}=\left[ \begin{array}{c} u \\ v \end{array} \right].</tex> <tex>\vec{u}=\left[ \begin{array}{c} u \\ v \end{array} \right].</tex>](lib/plugins/latex/images/712004a7a9662c525f6f577079d794031851b857_0.png)
![<tex>\vec{f}(t,u,v)=\left[ \begin{array}{c} v \\ -u-v \end{array} \right].</tex> <tex>\vec{f}(t,u,v)=\left[ \begin{array}{c} v \\ -u-v \end{array} \right].</tex>](lib/plugins/latex/images/dd8ae7da29796c11d2fbc976a1af14d6d5b664c2_0.png)
Entonces el problema es: ![<tex>\left\{ \begin{array}{rcl} \vec{u'}(t) & = & \vec{f}(t,u,v) \\ \vec{u}(0) & = & [1,1]^T \end{array}\right.</tex> <tex>\left\{ \begin{array}{rcl} \vec{u'}(t) & = & \vec{f}(t,u,v) \\ \vec{u}(0) & = & [1,1]^T \end{array}\right.</tex>](lib/plugins/latex/images/cd324de070a6c506504e0147dd6efe91d62c24dd_0.png)
Para responder a los V/F consideramos que 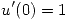 por dato de enunciado y por lo tanto
por dato de enunciado y por lo tanto 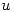 es creciente en
es creciente en  . Además
. Además 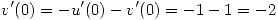 y entonces
y entonces  es decreciente en
es decreciente en  , y como
, y como  es
es 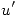 , por lo tanto
, por lo tanto 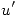 es decreciente en
es decreciente en  .
.
Con esto obtenemos:
- V
- F
- F
- V
Ahora vamos a calcular Euler-explícito, es decir: 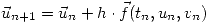
El ![<tex>\vec{u}_1=\vec{u}_0+h\cdot \vec{f}(t_0,u_0,v_0)=\left[\begin{array}{c} 1 \\ 1 \end{array}\right] + 0.1 \cdot \left[\begin{array}{c} 1 \\ -2 \end{array}\right]=\left[\begin{array}{c} 1.1 \\ 0.8 \end{array}\right]</tex> <tex>\vec{u}_1=\vec{u}_0+h\cdot \vec{f}(t_0,u_0,v_0)=\left[\begin{array}{c} 1 \\ 1 \end{array}\right] + 0.1 \cdot \left[\begin{array}{c} 1 \\ -2 \end{array}\right]=\left[\begin{array}{c} 1.1 \\ 0.8 \end{array}\right]</tex>](lib/plugins/latex/images/b6cbe79cfba755f18aee3d73228acecf9212bccb_0.png)
Por lo tanto 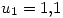 y
y 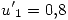
Ahora usaremos el método de Runge-Kutta, que para sistemas es: 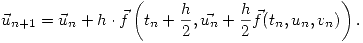
Vemos que ![<tex>\vec{f}(t_0,u_0,v_0)=\left[\begin{array}{c} 1 \\ -2 \end{array}\right]</tex> <tex>\vec{f}(t_0,u_0,v_0)=\left[\begin{array}{c} 1 \\ -2 \end{array}\right]</tex>](lib/plugins/latex/images/ccbd3e12e2d77a5f3c6e0421aec2ee86df3f9809_0.png) Entonces
Entonces ![<tex>\vec{u_0}+\frac{h}{2}\vec{f}(t_0,u_0,v_0)=\left[\begin{array}{c} 1 \\ 1 \end{array}\right]+0.05\cdot \left[\begin{array}{c} 1 \\ -2 \end{array}\right]=\left[\begin{array}{c} 1.05 \\ 0.9 \end{array}\right]</tex> <tex>\vec{u_0}+\frac{h}{2}\vec{f}(t_0,u_0,v_0)=\left[\begin{array}{c} 1 \\ 1 \end{array}\right]+0.05\cdot \left[\begin{array}{c} 1 \\ -2 \end{array}\right]=\left[\begin{array}{c} 1.05 \\ 0.9 \end{array}\right]</tex>](lib/plugins/latex/images/eaa8fa268b6bbb59dd5c8ed65638c74b45d6f113_0.png)
Entonces: ![<tex>\vec{u}_1=\left[\begin{array}{c} 1 \\ 1 \end{array}\right]+0.1\cdot \vec{f}(0,1.05,0.9)=\left[\begin{array}{c} 1 \\ 1 \end{array}\right]+0.1\cdot \left[\begin{array}{c} 0.9 \\ -1.95 \end{array}\right]=\left[\begin{array}{c} 1.09 \\ 0.805 \end{array}\right]</tex> <tex>\vec{u}_1=\left[\begin{array}{c} 1 \\ 1 \end{array}\right]+0.1\cdot \vec{f}(0,1.05,0.9)=\left[\begin{array}{c} 1 \\ 1 \end{array}\right]+0.1\cdot \left[\begin{array}{c} 0.9 \\ -1.95 \end{array}\right]=\left[\begin{array}{c} 1.09 \\ 0.805 \end{array}\right]</tex>](lib/plugins/latex/images/b4522ba0b4310e7520520081a47c85cdb5e445f8_0.png)
Por lo tanto con este método: 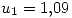 y
y 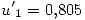
Para usar el método de Adams-Bashfort debemos usar antes los valores de 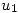 y
y 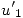 como valores de arranque calculados con otro de los métodos anteriores. Como este método de Adams-Bashfort es de orden 2, entonces usaremos el método de Runge-Kutta de orden 2. Es decir
como valores de arranque calculados con otro de los métodos anteriores. Como este método de Adams-Bashfort es de orden 2, entonces usaremos el método de Runge-Kutta de orden 2. Es decir ![<tex>\vec{u}_1=\left[\begin{array}{c} 1.09 \\ 0.805 \end{array}\right]</tex> <tex>\vec{u}_1=\left[\begin{array}{c} 1.09 \\ 0.805 \end{array}\right]</tex>](lib/plugins/latex/images/d75b90224235c4fc557c3e4c5646cfef36442810_0.png) . Entonces:
. Entonces:
![<tex>\vec{f}_0=\vec{f}(t_0,u_0,v_0)=\left[\begin{array}{c} 1 \\ -2 \end{array}\right]</tex> <tex>\vec{f}_0=\vec{f}(t_0,u_0,v_0)=\left[\begin{array}{c} 1 \\ -2 \end{array}\right]</tex>](lib/plugins/latex/images/6923cea9a6b2bdd8d53778ee84b5eadc8766a8ef_0.png)
![<tex>\vec{f}_1=\vec{f}(t_1,u_1,v_1)=\left[\begin{array}{c} 0.805 \\ -1.895 \end{array}\right]</tex> <tex>\vec{f}_1=\vec{f}(t_1,u_1,v_1)=\left[\begin{array}{c} 0.805 \\ -1.895 \end{array}\right]</tex>](lib/plugins/latex/images/10ca6b15a24723bebc9e715188eb59635fd99f61_0.png)
![<tex>\vec{u}_2=\left[\begin{array}{c} 1.09 \\ 0.805 \end{array}\right]+0.05\cdot \left( 3\cdot \left[\begin{array}{c} 0.805 \\ -1.895 \end{array}\right] - \left[\begin{array}{c} 1 \\ -2 \end{array}\right] \right)=\left[\begin{array}{c} 1.16075 \\ 0.62075 \end{array}\right]</tex> <tex>\vec{u}_2=\left[\begin{array}{c} 1.09 \\ 0.805 \end{array}\right]+0.05\cdot \left( 3\cdot \left[\begin{array}{c} 0.805 \\ -1.895 \end{array}\right] - \left[\begin{array}{c} 1 \\ -2 \end{array}\right] \right)=\left[\begin{array}{c} 1.16075 \\ 0.62075 \end{array}\right]</tex>](lib/plugins/latex/images/7cacd9c0d81a40470b1ad8211cf97678cf20a68c_0.png)
Por lo tanto con este método: 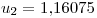 y
y