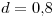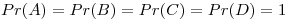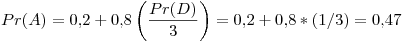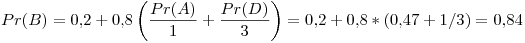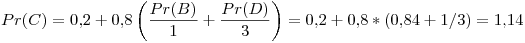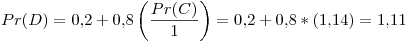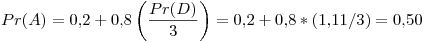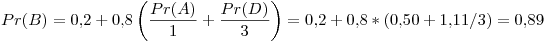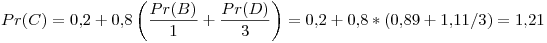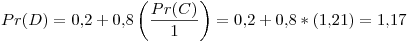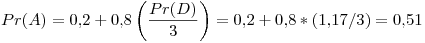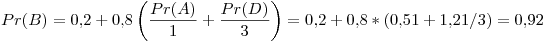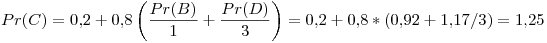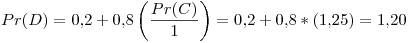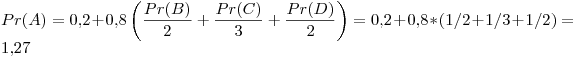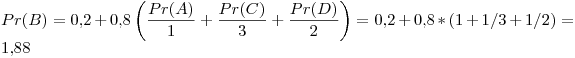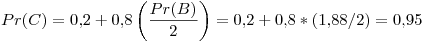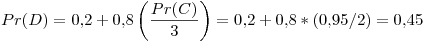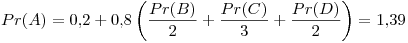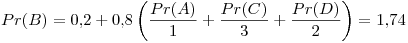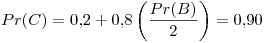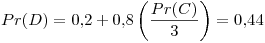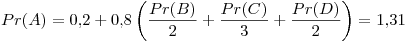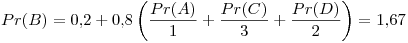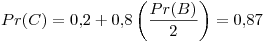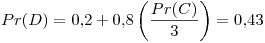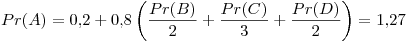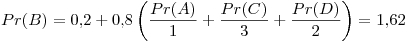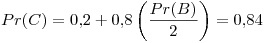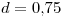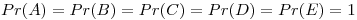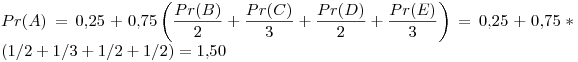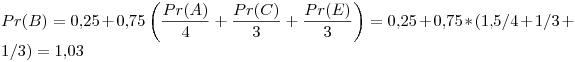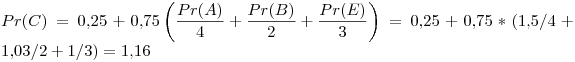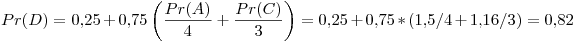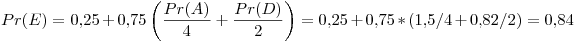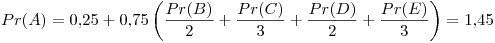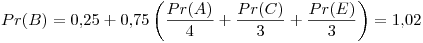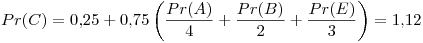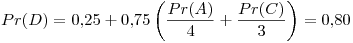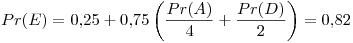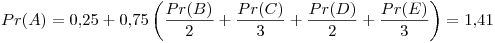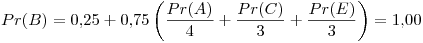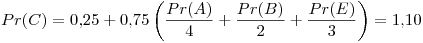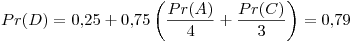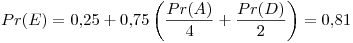Guía de ejercicios tomados en parciales y finales. [Foros-FIUBA::Wiki]

Guía de ejercicios tomados en parciales y finales.

Tema: Page Rank

Cátedra: Saubidet

Segundo Cuatrimestre de 2006. Examen parcial, segunda oportunidad: 16/11/2006.
Para un conjunto de 4 paginas web A,B,C,D con D=0,8 se pide calcular el page-rank de cada pagina luego de 3 iteraciones. Los links (desde,hasta) entre las paginas son:
(A,B) (B,C) (D,A) (D,B) (D,C) (C,D) (* *) (10 pts)

Criterio: Ej 7) Trivial
Primer Cuatrimestre de 2006. Examen parcial, primera oportunidad: 8/5/2006.
Si un buscador usa pagerank para ordenar la relevancia de los resultados obtenidos, explicar de que forma se podría intencionalmente mejorar el ranqueo de un determinado documento. (* * *) (10 pts)

Criterio: Ejercicio 7) Básicamente se debe responder que hay que aumentar la cantidad de links que apuntan a la pagina en cuestión, con la salvedad de que debe intentarse que las paginas que tienen mayor ranking apunten a la pagina que se quiere mejorar ya que esto incide mucho mas en el peso final de la pagina.
Primer Cuatrimestre de 2006. Examen parcial, tercera oportunidad y (2_2005_1P) Segundo Cuatrimestre de 2005. Examen parcial, primera oportunidad: 17/10/2005.
Sabiendo que cada par ordenado representa un link de tipo desde-hasta entre paginas se pide calcular el page-rank para cada pagina luego de 4 (cuatro) iteraciones.
(A,B) (B,A) (B,C) (C,D) (C,A) (C,B) (D,A) (D,B) (* *) (10 pts)

Criterio: Ejercicio 7: El valor de “d” lo pueden fijar arbitrariamente al igual que el ranking inicial de cada pagina siempre y cuando las paginas tengan el mismo ranking.
Primer Cuatrimestre de 2004. Examen parcial, primera oportunidad: 10/5/2004.
Dadas 5 páginas (P1,P2,P3,P4,P5) en donde los links existentes entre las páginas son los siguientes. (Cada par ordenado indica desde-hasta)
(P1,P2) (P1,P5) (P2,P3) (P3,P2) (P3,P4) (P4,P3) (P4,P5) (P5,P4) (P2,P1) (P3,P1) (P4,P1) (P5,P1).
Para d=0.75. Calcular el ranking de cada página usando Page-Rank realizando 3 iteraciones y comenzando con PR(X) =1. (10 pts) (*)
Recordar PR(x) = (1-d) + d * SUM (PRI1/CI1….PRIN/CIN)

Criterio: Ejercicio 7: Trivial, tomar todas las paginas y no solo las que linquean a la que se calcula descuenta 10 puntos.

Resueltos

Ej. 1

Comienzo con:

$<tex>d = 0.8</tex>$
$<tex> Pr(A)=Pr(B)=Pr(C)=Pr(D)=1</tex>$

Hasta ——– Desde	A	B	C	D	Salen	Llegan
A	-	1			1	D
B		-	1		1	A, D
C			-	1	1	B, D
D	1	1	1	-	3	C

Primer iteración:

$<tex> Pr(A) = 0.2 + 0.8\left( \frac{Pr(D)}{3} \right) = 0.2 + 0.8 * (1/3) = 0.47 </tex>$
$<tex> Pr(B) = 0.2 + 0.8\left( \frac{Pr(A)}{1} + \frac{Pr(D)}{3} \right) = 0.2 + 0.8 * (0.47 + 1/3) = 0.84 </tex>$
$<tex> Pr(C) = 0.2 + 0.8\left( \frac{Pr(B)}{1} + \frac{Pr(D)}{3} \right) = 0.2 + 0.8 * (0.84 + 1/3) = 1.14 </tex>$
$<tex> Pr(D) = 0.2 + 0.8\left( \frac{Pr(C)}{1} \right) = 0.2 + 0.8 * (1.14) = 1.11 </tex>$

Segunda iteración:

$<tex> Pr(A) = 0.2 + 0.8\left( \frac{Pr(D)}{3} \right) = 0.2 + 0.8 * (1.11/3) = 0.50 </tex>$
$<tex> Pr(B) = 0.2 + 0.8\left( \frac{Pr(A)}{1} + \frac{Pr(D)}{3} \right) = 0.2 + 0.8 * (0.50 + 1.11/3) = 0.89 </tex>$
$<tex> Pr(C) = 0.2 + 0.8\left( \frac{Pr(B)}{1} + \frac{Pr(D)}{3} \right) = 0.2 + 0.8 * (0.89 + 1.11/3) = 1.21 </tex>$
$<tex> Pr(D) = 0.2 + 0.8\left( \frac{Pr(C)}{1} \right) = 0.2 + 0.8 * (1.21) = 1.17 </tex>$

Tercer iteración:

$<tex> Pr(A) = 0.2 + 0.8\left( \frac{Pr(D)}{3} \right) = 0.2 + 0.8 * (1.17/3) = 0.51 </tex>$
$<tex> Pr(B) = 0.2 + 0.8\left( \frac{Pr(A)}{1} + \frac{Pr(D)}{3} \right) = 0.2 + 0.8 * (0.51 + 1.21/3) = 0.92 </tex>$
$<tex> Pr(C) = 0.2 + 0.8\left( \frac{Pr(B)}{1} + \frac{Pr(D)}{3} \right) = 0.2 + 0.8 * (0.92 + 1.17/3) = 1.25 </tex>$
$<tex> Pr(D) = 0.2 + 0.8\left( \frac{Pr(C)}{1} \right) = 0.2 + 0.8 * (1.25) = 1.20 </tex>$

Ej. 2

Para mejorar el ranqueo de un sitio en un buscador que use pagerank básicamente se pueden hacer tres cosas:

La más sencilla es aumentar el Page Rank de quien la apunta, o quitarle links a otras páginas para que no divida por tanto. Por ejemplo, si se quiere mejorar el Page Rank de A, quien solo es apuntada por B, pero a su vez, esta apunta a A, C, D y E.

En este caso podemos mejorar el Page Rank de B, o quitar las referencias a C, D y E para que divida su page rank por 1, en lugar de 4.
La segunda opción es agregar más páginas que la apunten, y en caso de tener que elegir, selecciono las que tengan mejor Page Rank. Por ejemplo, si quiero mejorar el de A, y solo la apunta B, entonces tengo que lograr que C, D y E también lo apunten.
La tercer opción es una combinación de las otras dos, es decir, mejorar el page rank de quienes apuntan a mi sitio, y lograr que más sitios lo apunten.

Ej. 3

Comienzo con:

$<tex>d = 0.8</tex>$
$<tex> Pr(A)=Pr(B)=Pr(C)=Pr(D)=1</tex>$

Desde Hasta	A	B	C	D	Salen	Llegan
A	-	1			1	B, C, D
B	1	-	1		2	A, C, D
C	1	1	-	1	3	B
D	1	1		-	2	C

Primer iteración:

$<tex> Pr(A) = 0.2 + 0.8\left( \frac{Pr(B)}{2} + \frac{Pr(C)}{3} + \frac{Pr(D)}{2} \right) = 0.2 + 0.8 * ( 1/2 + 1/3 + 1/2) = 1.27 </tex>$
$<tex> Pr(B) = 0.2 + 0.8\left( \frac{Pr(A)}{1} + \frac{Pr(C)}{3} + \frac{Pr(D)}{2} \right) = 0.2 + 0.8 * ( 1 + 1/3 + 1/2) = 1.88 </tex>$
$<tex> Pr(C) = 0.2 + 0.8\left( \frac{Pr(B)}{2} \right) = 0.2 + 0.8 * (1.88/2) = 0.95 </tex>$
$<tex> Pr(D) = 0.2 + 0.8\left( \frac{Pr(C)}{3} \right) = 0.2 + 0.8 * (0.95/2) = 0.45 </tex>$

Segunda iteración:

$<tex> Pr(A) = 0.2 + 0.8\left( \frac{Pr(B)}{2} + \frac{Pr(C)}{3} + \frac{Pr(D)}{2} \right) = 1.39 </tex>$
$<tex> Pr(B) = 0.2 + 0.8\left( \frac{Pr(A)}{1} + \frac{Pr(C)}{3} + \frac{Pr(D)}{2} \right) = 1.74 </tex>$
$<tex> Pr(C) = 0.2 + 0.8\left( \frac{Pr(B)}{2} \right) = 0.90 </tex>$
$<tex> Pr(D) = 0.2 + 0.8\left( \frac{Pr(C)}{3} \right) = 0.44 </tex>$

Tercer iteración:

$<tex> Pr(A) = 0.2 + 0.8\left( \frac{Pr(B)}{2} + \frac{Pr(C)}{3} + \frac{Pr(D)}{2} \right) = 1.31 </tex>$
$<tex> Pr(B) = 0.2 + 0.8\left( \frac{Pr(A)}{1} + \frac{Pr(C)}{3} + \frac{Pr(D)}{2} \right) = 1.67 </tex>$
$<tex> Pr(C) = 0.2 + 0.8\left( \frac{Pr(B)}{2} \right) = 0.87 </tex>$
$<tex> Pr(D) = 0.2 + 0.8\left( \frac{Pr(C)}{3} \right) = 0.43 </tex>$

Cuarta iteración:

$<tex> Pr(A) = 0.2 + 0.8\left( \frac{Pr(B)}{2} + \frac{Pr(C)}{3} + \frac{Pr(D)}{2} \right) = 1.27 </tex>$
$<tex> Pr(B) = 0.2 + 0.8\left( \frac{Pr(A)}{1} + \frac{Pr(C)}{3} + \frac{Pr(D)}{2} \right) = 1.62 </tex>$
$<tex> Pr(C) = 0.2 + 0.8\left( \frac{Pr(B)}{2} \right) = 0.84 </tex>$
$<tex> Pr(D) = 0.2 + 0.8\left( \frac{Pr(C)}{3} \right) = 0.43 </tex>$

Ej. 4

Para no confundirme con los subíndices, le cambio el nombre a los nodos según la siguiente tabla:

Nombre del enunciado	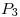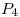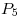$<tex>P_1</tex>$	$<tex>P_2</tex>$	$<tex>P_3</tex>$	$<tex>P_4</tex>$	$<tex>P_5</tex>$
Nuevo nombre	A	B	C	D	E

Comienzo con:

$<tex>d = 0.75 </tex>$
$<tex> Pr(A)=Pr(B)=Pr(C)=Pr(D)=Pr(E)=1</tex>$

Desde Hasta	A	B	C	D	E	Salen	Llegan
A	-	1	1	1	1	4	B, C, D, E
B	1	-	1	1		2	A, C, E
C	1	1	-			3	A, B, E
D	1			-	1	2	A, C
E	1	1	1		-	3	A, D

Primer iteración:

$<tex> Pr(A) = 0.25 + 0.75\left( \frac{Pr(B)}{2} + \frac{Pr(C)}{3} + \frac{Pr(D)}{2} + \frac{Pr(E)}{3} \right) = 0.25 + 0.75 * ( 1/2 + 1/3 + 1/2 + 1/2) = 1.50 </tex>$
$<tex> Pr(B) = 0.25 + 0.75\left( \frac{Pr(A)}{4} + \frac{Pr(C)}{3} + \frac{Pr(E)}{3} \right) = 0.25 + 0.75 * (1.5/4 + 1/3 + 1/3) = 1.03 </tex>$
$<tex> Pr(C) = 0.25 + 0.75\left( \frac{Pr(A)}{4} + \frac{Pr(B)}{2} + \frac{Pr(E)}{3} \right) = 0.25 + 0.75 * (1.5/4 + 1.03/2 + 1/3) = 1.16 </tex>$
$<tex> Pr(D) = 0.25 + 0.75\left( \frac{Pr(A)}{4} + \frac{Pr(C)}{3} \right) = 0.25 + 0.75 * (1.5/4 + 1.16/3) = 0.82 </tex>$
$<tex> Pr(E) = 0.25 + 0.75\left( \frac{Pr(A)}{4} + \frac{Pr(D)}{2} \right) = 0.25 + 0.75 * (1.5/4 + 0.82/2) = 0.84 </tex>$

Segunda iteración:

$<tex> Pr(A) = 0.25 + 0.75\left( \frac{Pr(B)}{2} + \frac{Pr(C)}{3} + \frac{Pr(D)}{2} + \frac{Pr(E)}{3} \right) = 1.45 </tex>$
$<tex> Pr(B) = 0.25 + 0.75\left( \frac{Pr(A)}{4} + \frac{Pr(C)}{3} + \frac{Pr(E)}{3} \right) = 1.02 </tex>$
$<tex> Pr(C) = 0.25 + 0.75\left( \frac{Pr(A)}{4} + \frac{Pr(B)}{2} + \frac{Pr(E)}{3} \right) = 1.12 </tex>$
$<tex> Pr(D) = 0.25 + 0.75\left( \frac{Pr(A)}{4} + \frac{Pr(C)}{3} \right) = 0.80 </tex>$
$<tex> Pr(E) = 0.25 + 0.75\left( \frac{Pr(A)}{4} + \frac{Pr(D)}{2} \right) = 0.82 </tex>$

Tercer iteración:

$<tex> Pr(A) = 0.25 + 0.75\left( \frac{Pr(B)}{2} + \frac{Pr(C)}{3} + \frac{Pr(D)}{2} + \frac{Pr(E)}{3} \right) = 1.41 </tex>$
$<tex> Pr(B) = 0.25 + 0.75\left( \frac{Pr(A)}{4} + \frac{Pr(C)}{3} + \frac{Pr(E)}{3} \right) = 1.00 </tex>$
$<tex> Pr(C) = 0.25 + 0.75\left( \frac{Pr(A)}{4} + \frac{Pr(B)}{2} + \frac{Pr(E)}{3} \right) = 1.10 </tex>$
$<tex> Pr(D) = 0.25 + 0.75\left( \frac{Pr(A)}{4} + \frac{Pr(C)}{3} \right) = 0.79 </tex>$
$<tex> Pr(E) = 0.25 + 0.75\left( \frac{Pr(A)}{4} + \frac{Pr(D)}{2} \right) = 0.81 </tex>$