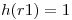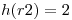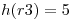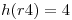Guía de ejercicios tomados en parciales y finales.
Tema: Funciones de Hashing y Archivos Directos.
Cátedra: Saubidet
- Primer Cuatrimestre de 2005. Examen parcial, primera oportunidad: 12/5/2005. y Segundo Cuatrimestre de 2005. Examen parcial, tercera oportunidad
c) Explique que es una función de hashing unidireccional y para que sirven las mismas. (*) (10 pts)
Criterio 2c2005: Ejercicio 3c: Tienen que decir fundamentalmente 2 cosas: que a partir del hash sea difícil encontrar la clave y también que sea difícil generar 2 claves que den el mismo hash (sinónimos). Si falta una de las 2 características vale la mitad.
Criterio 1c2005: Ej 3: d) Deben indicar tanto que debe ser difícil a partir de un hash obtener el registros como también debe ser difícil generar sinónimos, si falta alguna de las dos condiciones vale 0 puntos. Hay que indicar también brevemente para que se usan, si no lo hacen -5 puntos.
- Primer Cuatrimestre de 2004. Examen parcial, primer Recuperatorio: 31/5/2004.
c) Dado un archivo directo con buckets de 2 registros, con área de overflow distribuida (1 de overflow cada 2 de datos) y direccionamiento abierto lineal cíclico. Explique cómo se da de baja un registro. (10 pts) (*)
Criterio: Ejercicio 3: No requiere criterio por ser de tipo mecánico. Si hay algún error pero el método/procedimiento está bien, descontar 5 puntos. Si el procedimiento está mal vale 0 puntos.
- Primer Cuatrimestre de 2004. Examen parcial, primera oportunidad: 10/5/2004.
a) Explique el método de resolución de colisiones lineal cíclico con doble hashing sin área de overflow. (10 pts) (*)
Criterio: Ejercicio 3: No requiere criterio por ser de tipo mecánico. Si hay algún error pero el método/procedimiento está bien, descontar 5 puntos. Si el procedimiento está mal vale 0 puntos.
- Es el mismo ejercicio, pero con distintos enunciados y criterios:
- Primer Cuatrimestre de 2006. Examen parcial, primera oportunidad: 8/5/2006. (2_2006_1P)
4) Ejercicio previamente anunciado: Sean 5 strings S0..S4 usando M=7 se pide generar una función de hashing perfecta y mínima usando 2 funciones de hashing h1 y h2 indicando que es lo que debe almacenarse y como se usaría la función una vez generada. (* *) (15 pts)
Criterio 1c2006: Ejercicio 4) Trivial, si no explican como se usa la función de hashing o como se usa la misma se descuentan 10 puntos.
- Segundo Cuatrimestre de 2005. Examen parcial, primera oportunidad: 17/10/2005.
4) Usando 2 (dos) funciones de hashing y con M=7 construir una función de hashing perfecta y mínima para un total de 5 (cinco) strings. Explicar en cada paso como se construye la misma. Una vez construida la función explicar como se usa la misma. (* * *) (15 pts)
Criterio: Ejercicio 4: Si construye la función correctamente pero no explica como se usa vale como máximo 10 puntos.
- Segundo Cuatrimestre de 2005. Examen parcial, segunda oportunidad
6) Usando 2 (dos) funciones de hashing y con M=7 construir una función de hashing perfecta y mínima para un total de 5 (cinco) strings. Explicar en cada paso como se construye la misma. Una vez construida la función explicar como se usa la misma. (* * *) (10 pts)
Criterio: Ejercicio 6: Trivial, consiste en aplicar el método. Si no explican como se usa la función construida el ejercicio vale 0 (cero) puntos ya que mas allá de saber el método lo importante es saber para que sirve el mismo.
- Primer Cuatrimestre de 2004. Examen parcial, primera oportunidad: 10/5/2004.
4) (10 pts) (* *) Explique que diferencias existen entre los métodos de doble hashing, hashing lineal y cuadrático. ¿En que casos un método podría ser mejor que los otros dos?
Criterio: 4) Se debe explicar brevemente cada método y luego indicar ventajas y desventajas de cada uno. En lineas generales a menos que la explicación de los métodos sea completamente errada el ejercicio debería estar bien.
- Segundo Cuatrimestre de 2004. Examen parcial, segunda oportunidad: 4/11/2004.
5) Dar un ejemplo usando el método lineal, cuadrático de resolución de colisiones en el cual no sea posible dar de alta un registro pese a que existe espacio libre en el archivo directo. Indicar si este curioso caso puede detectarse y que se podría hacer para que las altas siempre estén garantizadas. (10 pts) (* *)
Criterio: 5) Simplemente se debe dar un ejemplo en el cual nunca se pase por un lugar libre. (5 puntos). Para detectar el problema se debe verificar si el factor de carga es mayor a 0,5 (2,5 puntos). Para evitarlo hay que reorganizar agregando registros al archivo directo (2,5 puntos)
- Primer Cuatrimestre de 2007. Examen parcial, primera oportunidad: 10/05/2007.
6) Sea un archivo directo usando doble hashing sin área de overflow independiente y sin encadenamiento de colisiones. Si se observa que la performance de las consultas realizadas al archivo no es satisfactoria. ¿que solución recomendaría? (* * *) (10 pts)
Criterio: Ejercicio 6: En primer lugar hay que analizar el factor de carga del archivo, si es muy alto lo mas recomendable es crear un archivo mayor y reorganizar. Si el factor de carga no fuera suficiente entonces el problema esta con la dispersión de las funciones de hashing, por lo que debería hacerse una reorganización in-situ cambiando una o ambas funciones de hashing.
- Primer Cuatrimestre de 2006. Examen parcial, segunda oportunidad
7) Explicar como influye el fenómeno conocido como “clustering“ en un archivo directo usando el método lineal, cuadrático o doblehashing.
Criterio: Ej 7) Trivial, explicar clustering, clustering secundario y como se resuelve esto usando doble-hashing.
- Primer Cuatrimestre de 2005. Examen parcial, primera oportunidad: 12/5/2004.
7) Explique como funcionan las altas en un archivo directo usando el método de resolución de colisiones cerrado con área de overflow independiente y buckets. (* * *) (10 pts)
Criterio: Ej 7) Es importante que expliquen que un bucket solo pueden co-existir sinónimos y como se manejan los encadenamientos y las altas en los distintos escenarios posibles.
Resueltos
Ej 1.
Las funciones de hashing unidireccionales son, valga la redundancia, funciones que al aplicárselas a una clave o mensaje (M) retorna un valor dado. Además, debe cumplir con 3 características específicas:
- dado M, debe ser muy fácil encontrar h(M).
- dado h(M), debe ser muy difícil encontrar M.
- dado h(M), debe ser muy difícil encontrar un sinónimo, es decir un M' tal que h(M)=h(M').
El uso principal es para firmas digitales, encriptar datos y archivos.
Ej 3.
El método de resolución de colisiones lineal, cíclico, con doble hashing y sin área de overflow mezcla los registros que se encuentran en su posición con los que buscaron posiciones alternativas por encontrarse su posición ocupada. Es decir, los datos se almacenan en el mismo espacio que los sinónimos. Además, al no usar buckets, solo se almacena un registro por posición.
Como el método es lineal, cíclico y con doble hashing lo primero que se hace al encontrar una colisión es buscar el registro siguiente y, en caso de estar ocupado, se aplica otra función de hashing. (o sería al revés?, al encontrar una colisión buscaría en otra posición con la segunda función de hashing y después en forma lineal).
Ej 4.
Construyo 2 funciones de hashing para aplicarle a los strings, con un espacio de direcciones contenido en [0 - M-1]
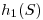 | 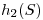 | 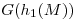 | 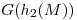 | 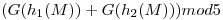 |
|
|---|---|---|---|---|---|
| S0 | 0 | 1 | |||
| S1 | 5 | 3 | |||
| S2 | 4 | 0 | |||
| S3 | 3 | 2 | |||
| S4 | 6 | 2 |
Armo un grafo con los M-1 nodos.

Uno los nodos del grafo según las funciones de hashing definidas anteriormente y nombro las aristas según el string al que corresponden esos valores.





Verifico que no tenga ciclos y rotulo un nodo a elección con un valor en particular; por ejemplo, el nodo 0 con el valor 0.

Luego, para cada nodo vecino le asigno el rótulo dado por la cuenta: 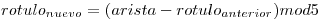
Para el nodo 1: 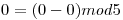

Para el nodo 4: 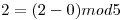

Como ya no tengo nodos vecinos, rotulo aleatoriamente un nuevo nodo. Por ejemplo, el nodo 2 con el valor 0.

Si rotulando como antes, para el nodo 6: 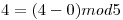

Para el nodo 3: 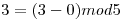

Y por último, para el nodo 5: 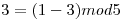

Con esto construyo una nueva función de hashing, G(x), la cual tendrá para cada nodo del grafo su rótulo asociado:
| x | G(x) |
|---|---|
| 0 | 0 |
| 1 | 0 |
| 2 | 0 |
| 3 | 3 |
| 4 | 2 |
| 5 | 3 |
| 6 | 4 |
Ahora sigo completando la tabla. Primero le aplico la función de hashing 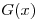 a los valores retornados por
a los valores retornados por 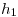 y
y 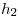 :
:
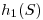 | 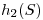 | 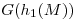 | 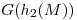 | 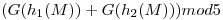 |
|
|---|---|---|---|---|---|
| S0 | 0 | 1 | 0 | 0 | |
| S1 | 5 | 3 | 3 | 3 | |
| S2 | 4 | 0 | 2 | 0 | |
| S3 | 3 | 2 | 3 | 0 | |
| S4 | 6 | 2 | 4 | 0 |
Y por último, sumo los valores de 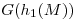 con
con 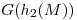 , terminando al aplicar módulo 5 al resultado.
, terminando al aplicar módulo 5 al resultado.
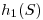 | 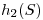 | 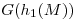 | 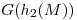 | 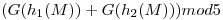 |
|
|---|---|---|---|---|---|
| S0 | 0 | 1 | 0 | 0 | 0 |
| S1 | 5 | 3 | 3 | 3 | 1 |
| S2 | 4 | 0 | 2 | 0 | 2 |
| S3 | 3 | 2 | 3 | 0 | 3 |
| S4 | 6 | 2 | 4 | 0 | 4 |
Lo que tengo que guardar es 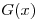 ,
, 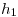 y
y 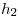 . Para usarlo le aplico
. Para usarlo le aplico 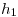 y
y 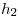 al string, luego
al string, luego 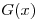 a los resultados terminando con módulo 5:
a los resultados terminando con módulo 5:
![<tex> pos = ( G[h_1(s)] + G[h_2(s)] ) mod 5 </tex> <tex> pos = ( G[h_1(s)] + G[h_2(s)] ) mod 5 </tex>](lib/plugins/latex/images/0c8e09b148f3d3c672a203092ac609204807f7a7_0.png)
Por ejemplo, para S3:
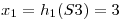
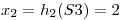
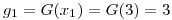
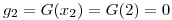
pos 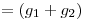 mod
mod 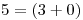 mod
mod 
Ej 5.
Existen varios métodos de resolución de colisiones entre los que se encuentran hashing lineal, hashing cuadrático y doble hashing. En estos 3 métodos la posición a la que queremos acceder viene dada por la función: 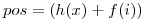 mod
mod  , con
, con 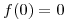 .
.
Es decir, que la posición depende de una función de hashing 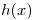 y una función auxiliar
y una función auxiliar 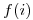 , donde
, donde 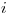 es el número de intento por encontrar la posición comenzando en
es el número de intento por encontrar la posición comenzando en  . Al final se le aplica mod
. Al final se le aplica mod  para que la suma caiga en el espacio de direcciones. Esa función
para que la suma caiga en el espacio de direcciones. Esa función 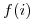 es la que va a variar en los 3 casos.
es la que va a variar en los 3 casos.
Para la resolución de colisiones lineal 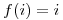 , lo que significa que en primer lugar accede a la posición dada por la función de hashing; y en caso de una colisión se accede al elemento siguiente, y si nuevamente hay una colisión busca en el siguiente, y así sucesivamente hasta encontrar una posición libre. Al llegar al final del archivo, comienza por la primer posición. La ventaja es que si existe un lugar vacío, el método lo va encontrar. Sin embargo, la desventaja es que debido a que los sinónimos y los registros vecinos producirán las mismas posiciones a probar se produce un aglomeramiento de registros llamado clústering. Esto es perjudicial porque hace que tengamos áreas densamente pobladas, y otras vacías.
, lo que significa que en primer lugar accede a la posición dada por la función de hashing; y en caso de una colisión se accede al elemento siguiente, y si nuevamente hay una colisión busca en el siguiente, y así sucesivamente hasta encontrar una posición libre. Al llegar al final del archivo, comienza por la primer posición. La ventaja es que si existe un lugar vacío, el método lo va encontrar. Sin embargo, la desventaja es que debido a que los sinónimos y los registros vecinos producirán las mismas posiciones a probar se produce un aglomeramiento de registros llamado clústering. Esto es perjudicial porque hace que tengamos áreas densamente pobladas, y otras vacías.
Una forma de solucionar este problema es cambiar la función auxiliar 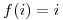 por
por 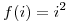 , que es lo que usa el método de resolución de colisiones cuadrático . De esta forma eliminamos los clústering, ya que ahora las posiciones vecinas no producirán el mismo patrón de búsqueda. Ante la primer colisión accedemos a la siguiente posición (
, que es lo que usa el método de resolución de colisiones cuadrático . De esta forma eliminamos los clústering, ya que ahora las posiciones vecinas no producirán el mismo patrón de búsqueda. Ante la primer colisión accedemos a la siguiente posición (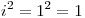 ), luego nos alejamos un poco más a 4 lugares de distancia (
), luego nos alejamos un poco más a 4 lugares de distancia (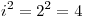 ), luego 9 lugares (
), luego 9 lugares (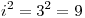 ), y así alejándonos cada vez más. Como dijimos antes, la ventaja es que eliminamos el clústering, pero generamos clústering secundario, que son aglomeraciones de registros, pero menos densas y más distribuidas (cosa que perjudica a la cache). Además, es posible que existan posiciones libres y no las encuentre, ya que puedo ir saltando siempre entre las mismas posiciones. Para esto último hay un teorema que dice que si el factor de carga es menor a 0.5 y
), y así alejándonos cada vez más. Como dijimos antes, la ventaja es que eliminamos el clústering, pero generamos clústering secundario, que son aglomeraciones de registros, pero menos densas y más distribuidas (cosa que perjudica a la cache). Además, es posible que existan posiciones libres y no las encuentre, ya que puedo ir saltando siempre entre las mismas posiciones. Para esto último hay un teorema que dice que si el factor de carga es menor a 0.5 y  es primo, entonces, si existe un lugar libre lo encuentro si o si.
es primo, entonces, si existe un lugar libre lo encuentro si o si.
Para solucionar el clústering secundario se usa el método de resolución de colisiones con doble hashing , que consiste en que 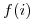 sea otra función de hashing:
sea otra función de hashing: 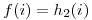 . De esta forma los sinónimos no necesariamente siguen la misma secuencia de posiciones a probar. Si la segunda posición a probar también estuviera ocupada podría continuarse en forma lineal, cuadrática, random o con otra función de hashing.
. De esta forma los sinónimos no necesariamente siguen la misma secuencia de posiciones a probar. Si la segunda posición a probar también estuviera ocupada podría continuarse en forma lineal, cuadrática, random o con otra función de hashing.
Entonces, la principal diferencia entres estos 3 métodos radica en la función 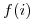 , que puede ser
, que puede ser 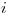 ,
, 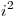 , o
, o 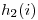 . Esto tiene como efecto que el método lineal genera áreas localizadas muy densas de registros muchas otras con densidades casi nulas. Mientras que el método cuadrático produce clústering secundario que es aglomeramiento, pero no tanto y más disperso, y no siempre garantiza encontrar una posición libre. El método de doble hashing soluciona los problemas de ambos y puede combinarse con ellos.
. Esto tiene como efecto que el método lineal genera áreas localizadas muy densas de registros muchas otras con densidades casi nulas. Mientras que el método cuadrático produce clústering secundario que es aglomeramiento, pero no tanto y más disperso, y no siempre garantiza encontrar una posición libre. El método de doble hashing soluciona los problemas de ambos y puede combinarse con ellos.
En el caso de que las probabilidades de ocurrencia de los registros sean equivalente y el resultado de la primer función de hashing aplicado al espacio de claves de un resultado uniforme, elegiría el método lineal para tener los sinónimos cerca y aprovechar las optimizaciones de la cache. Si la distribución de la función de hashing es uniforme, pero es más probable que aparezcan ciertas claves, como podría ser al aplicar div 100 a los padrones de los alumnos que cursan una materia. Obviamente los más altos serán más probables y cuanto más chico sea el padrón , menor será la posibilidad de que aparezca un padrón de ese rango. En este caso usaría el de doble hashig, tal vez combinado con el método cuadrático.
Ej 6.
Con  y si:
y si:
| pos | registro |
|---|---|
| 0 | |
| 1 | r1 |
| 2 | |
| 3 | |
| 4 | |
| 5 |
| pos | registro |
|---|---|
| 0 | |
| 1 | r1 |
| 2 | r2 |
| 3 | |
| 4 | |
| 5 |
| pos | registro |
|---|---|
| 0 | |
| 1 | r1 |
| 2 | r2 |
| 3 | |
| 4 | |
| 5 | r3 |
| pos | registro |
|---|---|
| 0 | |
| 1 | r1 |
| 2 | r2 |
| 3 | |
| 4 | r4 |
| 5 | r3 |
- Si ahora quiero guardar r5 con
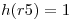 , veo que tengo una colisión, entonces analizo las siguientes opciones:
, veo que tengo una colisión, entonces analizo las siguientes opciones:
| intento | 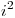 | 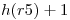 | 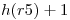 mod mod  |
|---|---|---|---|
| 0 | 0 | 1 | 1 (ocupado) |
| 1 | 1 | 2 | 2 (ocupado) |
| 2 | 4 | 5 | 5 (ocupado) |
| 3 | 9 | 10 | 4 (ocupado) |
| 4 | 16 | 17 | 5 (ocupado) |
| 5 | 25 | 26 | 2 (ocupado) |
| 6 | 36 | 37 | 1 (ocupado) |
| 7 | 49 | 50 | 2 (ocupado) |
| 8 | 64 | 65 | 5 (ocupado) |
| 9 | 81 | 82 | 4 (ocupado) |
Para corroborar que funciona con 10.000.000 de intentos, podemos correr el siguiente código python:
max = 10000000 valores = [1, 2, 4, 5] for i in range(0, max): if not ((i**2 + 1) % 6 in valores): print "Error %d" % i
En este caso vemos que el factor de carga 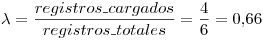 (mayor a 0.5) y que la cantidad de registros totales (N) es un número par (6). Esas serían las cosas que pueden ayudar a darse cuenta si es posible no encontrar una posición libre, por más que exista. Lo primero que hay que modificar es tener siempre una cantidad de registros totales impar, en este caso podría ser 7. Luego, ante cada inserción hay que controlar que el factor de carga sea menor a 0.5; si en algún momento
(mayor a 0.5) y que la cantidad de registros totales (N) es un número par (6). Esas serían las cosas que pueden ayudar a darse cuenta si es posible no encontrar una posición libre, por más que exista. Lo primero que hay que modificar es tener siempre una cantidad de registros totales impar, en este caso podría ser 7. Luego, ante cada inserción hay que controlar que el factor de carga sea menor a 0.5; si en algún momento  pasa ese valor hay que extender el archivo hasta el siguiente número primo. Esto es así ya que esta demostrado que si N es primo y el factor de carga es menor a 0.5 el método encontrará un lugar libre en caso de existir.
pasa ese valor hay que extender el archivo hasta el siguiente número primo. Esto es así ya que esta demostrado que si N es primo y el factor de carga es menor a 0.5 el método encontrará un lugar libre en caso de existir.
Ej 7.
En primer lugar analizaría el factor de carga del archivo; si es muy alto lo más recomendable es crear uno nuevo y reorganizarlo. Si el factor de carga es menor a 0.5 el error es del método de resolución de colisiones. Puede ajustarse mejor el método al caso de uso al cambiar una o ambas funciones de hashing, también puede cambiarse parcialmente (agregar un área de overflow distribuida y/o con encadenamiento de sinónimos) o en forma completa (pasar a usar un método lineal con encadenamiento de sinónimos).
Ej 8.
El cústering es una gran aglomeración de registros en áreas particularmente definidas, dejando una densidad muy baja (casi nula) en el resto del archivo. Suele producirse cuando se usa el método de resolución de colisiones lineal y se insertan una gran cantidad de sinónimos.
El método cuadrático elimina el clústering al recorrer el archivo con saltos cada vez más grandes; pero provoca el clústering secundario que también es una aglomeración de registros pero no tantos y más dispersos en el archivo.
Para solucionar ambos problemas se usa el método de doble hashing al no seguir la serie de posiciones a probar para todos los sinónimos.
Ej 9.
Cuando se quiere dar una alta en este tipo de archivos lo primero que se hace es aplicarle la función de hashing a la clave del registro y hacer un acceso directo a esa posición. Se observa si el bucket tiene espacio para un registro más, y en caso de ser así se lo coloca y actualiza la cantidad de registros en el bucket. Si el bucket estaba lleno y el offset es 0 significa que no hay más sinónimos en el archivo, por lo que se busca un bucket libre en el área de overflow, se lo almacena allí, se pone el contador de registros ocupados en 1 y se referencia desde la posición original al nuevo bucket. No se puede usar uno que ya se este usando pero tenga espacio ya que en un bucket solo pueden coexistir sinónimos y este no sería el caso ya que antes dijimos que no había más sinónimos en el archivo. Si el offset era distinto de cero, entonces accedo a la posición indicada y sigo la lista hasta encontrar el último bucket encadenado. En este momento, podemos encontrarnos con dos situaciones: que este bucket tenga espacio para el registro o que se encuentre lleno. Si tenía espacio lo guardo y actualizo el contador de registros ocupados. Si estaba lleno, busco un bucket libre en el cual guardo el registro y actualizo los datos administrativos. Si en alguno de los dos casos en que buscaba un bucket libre el área de overflow estaba llena, retorno un error.