Guía de ejercicios tomados en parciales y finales. [Foros-FIUBA::Wiki]

Guía de ejercicios tomados en parciales y finales.

Tema: Codificación de números

Cátedra: Saubidet

Segundo Cuatrimestre de 2006. Examen parcial, segunda oportunidad: 16/11/2006.
a) Un código prefijo siempre decodificable. (* *) (10 pts)

Criterio: Ej 3a) Verdadero. Al ser prefijo no pueden presentarse ambigüedades en la decodificación.
Primer Cuatrimestre de 2006 y Segundo Cuatrimestre de 2005. Examen parcial, primera oportunidad: 17/10/2005. Examen parcial, tercera oportunidad
a) Usando b=5 representar usando códigos de Golomb los siguientes numeros: 98, 171, 23, 33 (*) (10 pts)

Criterio: Trivial
b) Dar un ejemplo de un código prefijo que no sea decodificable. (*) (10 pts)

Criterio: Ejercicio 3b: No es posible, con decir que lo pedido es imposible alcanza.
Ej 6 Primer Cuatrismestre de 2006. Examen parcial, tercera oportunidad y 3 c del Segundo Cuatrimestre de 2005. Examen parcial, primera oportunidad: 17/10/2005.
c) Dar un ejemplo de un código que sea decodificable y no sea prefijo para 5 símbolos. (10 pts) (* *)

Criterio:
Ejercicio 3: c) Si el código es prefijo vale 0 puntos.
Primer Cuatrimestre de 2005. Examen parcial, primera oportunidad: 12/5/2004.
a) Usando códigos de Golomb con b=4 representar los siguientes números: 23,51,77 (*) (10 pts)

Criterio: Ej 3: a) Trivial
Primer Cuatrimestre de 2005. Examen parcial, primera oportunidad: 12/5/2004.
c) Representar usando código delta los siguientes números: 77,21,83 (*) (10 pts)

Criterio: Ej 3: c) Trivial
(2_2004_1P_1R) Primer Cuatrimestre de 2004. Examen parcial, segunda oportunidad: 4/11/2004.
a) Representar los siguientes números usando código delta: 27,0,71,3 (* *) (10 pts)

Criterio: 3) a) Trivial notando que el 0 no se puede representar en Delta (0,25 c/u)
(2_2004_1P_1R) Primer Cuatrimestre de 2004. Examen parcial, segunda oportunidad: 4/11/2004.
b) Indicar si el siguiente código es decodificable: A=01, B=011, C=111 (* *) (10 pts)

Criterio: b) Si dice que no porque no es prefijo esta mal (0 puntos). Si dice que no y da un contraejemplo esta bien siempre y cuando el contraejemplo funcione (es decir que no se pueda decodificar). Si dice que si indicando que pese a no ser prefijo es imposible construir una secuencia que no se pueda decodificar esta bien.
Primer Cuatrimestre de 2004. Examen parcial, primer Recuperatorio: 31/5/2004. a) Representar usando códigos de Golomb para b=7 los números 223,17 y 31. (*) (10 pts)

Criterio: Ejercicio 3: No requiere criterio por ser de tipo mecánico. Si hay algún error pero el método/procedimiento está bien, descontar 5 puntos. Si el procedimiento está mal vale 0 puntos.
Primer Cuatrimestre de 2004. Examen parcial, primera oportunidad: 10/5/2004.
c) Utilizar códigos de Golomb con b=5 para codificar los siguientes números: 3,1,22,151. (10 pts) (*)

Criterio: Ejercicio 3: No requiere criterio por ser de tipo mecánico. Si hay algún error pero el método/procedimiento está bien, descontar 5 puntos. Si el procedimiento está mal vale 0 puntos.
(2_2005_1P_1R) Segundo Cuatrimestre de 2005. Examen parcial, segunda oportunidad
4) Un horno industrial debe trabajar a una temperatura de 1500°C en forma constante. Previendo esto se instala un sensor que monitorea la temperatura cada segundo y la envía a la sala de control. El sensor instalado tiene una máxima sensibilidad de 1 décima de grado. Proponga un algoritmo que permita comprimir la información de temperatura, teniendo en cuenta que esta se envía cada segundo la medición y que durante ese tiempo la temperatura varía como mucho en 1 grado. (* * * *) (15 pts)

Criterio: Ejercicio 4: En primer lugar debe quedar claro que almacenar temperaturas no tiene sentido ya que puede almacenarse la temperatura inicial y luego las diferencias. Como las diferencias oscilan entre 0,1 y 1 el problema se reduce a almacenar números de 0 a 9 o dicho de otra forma 10 valores posibles por segundo. El método elegido debe basarse en esto para comprimir eficientemente. Hay infinitas soluciones correctas por lo que se debe evaluar la calidad de la solución presentada en forma cualitativa.

Ej. 1

Verdadero: Al ser prefijo no se pueden presentar ambigüedades, por lo que siempre se va a poder decodificar.

Código de Golomb con b=5:
$<tex> G(x) = U(q+1)+pref(r) </tex>$ donde: $<tex> \left\{ \begin{array}{l} U(q+1) \mbox { es la representacion en unario del numero } q+1. \\pref(r) \mbox { es la representacion en un codigo prefijo del numero } r. \\Q \mbox{ se calcula como:} Q = \lfloor \frac{x-1}{b} \rfloor \\r \mbox{ se calcula como:} r = x-1-q*b\end{array} \right. </tex>$
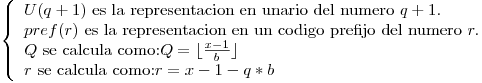
Los códigos prefijos los saco de un árbol binario y quedaría como:

x	pref(x)
0	00
1	01
2	10
3	110
4	111

x	Q	U(Q+1)	r(X)	pref(r(x))	G(x)
23	4	00001	2	10	0000110
33	6	0000001	2	10	000000110
98	19	00000000000000000001	2	10	0000000000000000000110
171	34	00000000000000000000000000000000001	0	00	0000000000000000000000000000000000100

Ej. 3

No es posible ya que el código es prefijo, si o si es decodificable.

Ej. 4

x	pref(x)
0	0001
1	00010
2	100
3	10
4	11

No es prefijo ya que el 0 es igual al comienzo del 1, pero no encontre ningún ejemplo en que al decodificar encuentre una ambigüedad.

Ej. 5

Código de Golomb con b=4:
$<tex> G(x) = U(q+1)+pref(r) </tex>$ donde: $<tex> \left\{ \begin{array}{l} U(q+1) \mbox { es la representacion en unario del numero } q+1. \\pref(r) \mbox { es la representacion en un codigo prefijo del numero } r. \\Q \mbox{ se calcula como:} Q = \lfloor \frac{x-1}{b} \rfloor \\r \mbox{ se calcula como:} r = x-1-q*b\end{array} \right. </tex>$
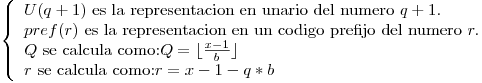
Los códigos prefijos los saco de un árbol binario y quedaría como:

x	pref(x)
0	00
1	01
2	10
3	11

x	Q	U(Q+1)	r(X)	pref(r(x))	G(x)
23	5	000001	2	10	00000110
51	12	0000000000001	2	10	000000000000110
71*	17	000000000000000001	2	10	00000000000000000110
77	19	00000000000000000001	0	00	0000000000000000000100

*: El de 71 no lo pedía, pero cuando lo hice me confundí, así que ya que lo tenía hecho lo puse igual.