Tabla de Contenidos
Examen Final - 71.15. Modelos y Optimización II
Cátedra: Markdorf
Fecha: Todas
Esta página está incompleta; podés ayudar completando el material.
Teoría de Colas
Gestión de Stocks
- Definición del Problema de Stocks.
- Explicar reposición a períodos frecuentes y reposición a cantidades fijas. Decidir y explicar qué método le aplicarías a un ítem A de la curva ABC.
- Si se tienen dos modelos de stock, uno el básico (alternativa 1) y el otro el básico con agotamiento (alternativa 2), responder justificando cual cree es la respuesta correcta:
- Conviene siempre la alternativa 1, salvo un único caso.
- Conviene siempre la alternativa 2, salvo un único caso.
- Depende la situación conviene la alternativa 1 o la alternativa 2.
- Demostrar matemáticamente que el costo total de órdenes iguala al costo total de compra, cuando se utiliza el lote óptimo de compra en un modelo de tipo 1 (sin agotamiento permitido, sin stock de seguridad, etc.).
Camino Crítico
- Definir el objetivo de la Programación por Camino Crítico.
- Definición de camino crítico.
- Detallar la totalidad de ventajas de la utilización de programación por Camino Crítico para planificación y control de proyectos, en relación al uso del diagrama GANTT.
- Decir si es V o F o a medias, lo siguiente: “una tarea es critica si está entre dos nodos críticos”.
- Enunciar la metodología de reducción de actividades en un proyecto en donde se establece el costo directo de cada actividad.
Simulación
- Diferencias entre los métodos analíticos y simulación (del apunte que está en la web).
- Definición y cuándo utilizarías el proceso de “evento a evento” o el de “tiempos fijos” y por qué conviene.
- Explicar al menos dos lenguajes de simulación y sus principales características.
- Ejercicio de colas con dos canales. La distribución de arribos es Poisson con media 2 clientes por hora, la distribución de atención del canal 1 es exponencial con tiempo de servicio 0,8hs. por cliente y la del canal 2 es uniforme con a = 0,3hs. Y b = 0,8hs. Se dan cinco valores aleatorios para arribos, cinco para el canal 1 y cinco para el canal 2. Se deben simular cinco arribos y sus salidas mediante el método evento a evento y calcular:
- Cantidad de clientes rechazados.
- Tiempo promedio en sistema de los clientes atendidos.
- Tiempo en que el canal 1 estuvo bloqueado.
- Explicar el método congruencial mixto para la generación de números aleatorios.
Resolución
Gestión de Stocks
- Problema de stocks: es aquel en el que se requiere determinar las cantidades y oportunidades en que se debe obtener, comprar, producir y almacenar uno o varios elementos con el objetivo de satisfacer su futura demanda.
- Períodos frecuentes.
- Conviene siempre la alternativa 2, salvo un único caso.
- Se debe demostrar que
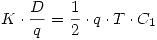 . Sabiendo que:
. Sabiendo que: 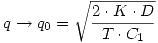 . Además, recordar que
. Además, recordar que 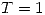
Camino Crítico
- Objetivo de la Programación por Camino Crítico: Planeamiento, programación y posterior control de la ejecución de proyectos, proveyendo los elementos de decisión cuantificados, que permitan seleccionar planes, programas y además, en la etapa de control, tomar las decisiones óptimas para cada situación.
- Camino crítico: secuencia ininterrumpida de actividades críticas. Un retraso en cualquiera de las actividades críticas retrasará todo el proyecto.
- El diagrama de Gannt tiene dos desventajas:
- El planeamiento y programación se hacen al mismo tiempo.
- No se ve claramente la relación entre las variables.
- Es verdad a medias porque además el margen total de la tarea crítica debe ser 0.
- Se debe seleccionar la actividad crítica con menor costo de reducción por día. Se ve en cuánto se debe reducir la actividad y se recalcula toda la red con la nueva duración.
Simulación
- Método congruencial mixto: En la actualidad se utilizan casi exclusivamente los métodos denominados “de congruencia”, o congruenciales lineales, que se generan a partir del módulo de los números que se van obteniendo. El módulo implica realizar la división por dicho valor, y tomar como resultado de la operación el resto o residuo de la división. En el generador congruencial mixto, la relación de recurrencia es:
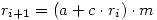 , donde
, donde  es la semilla del generador (el número inicial),
es la semilla del generador (el número inicial),  es la constante aditiva,
es la constante aditiva,  es la constante multiplicativa y
es la constante multiplicativa y  es la constante módulo, que debe ser mayor a
es la constante módulo, que debe ser mayor a  , mayor a
, mayor a  y mayor a
y mayor a  .
.
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
