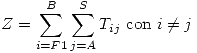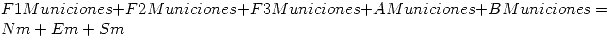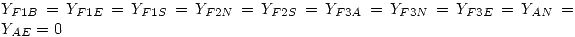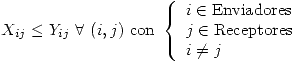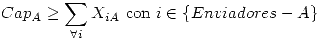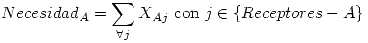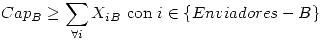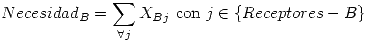Examen Final - 71.14. Modelos y Optimización I
Cátedra: Todas
Fecha: Primer Cuatrimestre 2004 - 1ra Oportunidad
Día: 17/07/2004
Enunciado
Punto A
La Francia es libre, la revolución está en marcha, pero los países vecinos, gobernados por reyes, la atacan para sacarle territorio y restaurar la monarquía. Pero la revolución se defiende, tiene buenos generales, uno de ellos, muy joven, que es el mejor de todos. Ahora se trata de abastecer de municiones a los ejércitos que combaten en el norte, este y sur. Cuentan con tres fundiciones (las denominaremos F1, F2 y F3). Existen también dos puntos estratégicos desde los cuales se pueden enviar suministros a los ejércitos (a estos puntos los denominaremos A y B). La tabla que damos a continuación nos indica el tiempo necesario (en días) para mover los suministros desde el lugar i hasta el lugar j:
| Puesto A | Puesto B | Ej. Norte | Ej. Este | Ej. Sur | Cap. Máxima de Despacho | |
|---|---|---|---|---|---|---|
| F1 | d1 | - | d7 | - | - | Cap1 |
| F2 | d2 | d4 | - | d9 | - | Cap2 |
| F3 | - | d5 | - | - | d11 | Cap3 |
| A | - | d6 | - | - | d12 | Cap4 |
| B | d3 | - | d8 | d10 | d13 | Cap5 |
Cuando no se indica valor es porque no es factible hacer ese recorrido, la última columna nos indica la capacidad máxima de despacho de cada uno de los lugares, en toneladas. En F1 disponemos de F1municiones, en F2 de F2municiones y en F3 se dispone de F3municiones (todos estos datos en toneladas), Asimismo en A disponemos de Amuniciones y en B de Bmuniciones (también en toneladas). Los ejércitos norte, este y sur requieren, urgentemente, Nm, Em y Sm toneladas de municiones.
¿Qué es lo mejor que se puede hacer con la información disponible? Se pide:
A.1
Análisis del problema, Objetivo completo y claro. Hipótesis necesarias para su resolución (al menos tres). Modelo de programación lineal para su resolución óptima.
Resolución
Punto A
A.1
Este es un típico problema de Distribución con Transbordos, con dos particularidades:
- Los transbordos intercambian entre sí
- Hay caminos que no se pueden utilizar
Objetivo: Determinar la cantidad de municiones a enviar desde cada Fundición y cada Punto Estratégico hacia cada Punto Estratégico o Ejército, a fin de minimzar los tiempos de transporte.
Hipótesis:
Definición de conjuntos:
- Enviadores = {F1,F2,F3,A,B}
- Receptores = {A,B,N,E,S}
Variables Utilizadas:
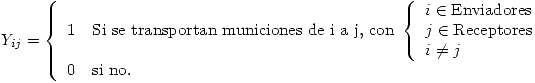
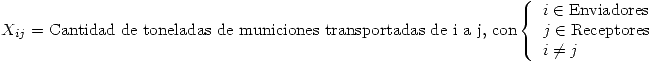
Restricciones:
Con esta restricción se logra que los caminos que actualmente están vedados puedan ser utilizados en otro momento por este mismo modelo (o caminos que actualmente son permitidos estén vedados). Esta restricción, además, permite plantear el resto del problema sin preocuparse por cuáles Enviadores pueden abasatecer a cuáles Receptores. Cabe destacar que si bien el problema va a tener más restricciones y más variables, también será más reutilizable: sólo modificando esta restricción y la tabla de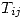 
puede considerarse cualquier eventualidad.
Esta restricción evita que se envíen municiones desde un Enviador a un Recpetor que no están conectados.
Estas restricciones hacen que todos los Receptores reciban lo que necesitan y que los Enviadores envían todo lo que tienen:
Funcional (MIN):
