Ejercicio de Parcial de Modelización - 71.07. Investigación Operativa
Cátedra: Miranda
Enunciado
En una empresa se reúnen los departamentos de Marketing y Ventas para definir el pronóstico trimestral de ventas de un cierto producto para el año próximo, quedando definidas las siguientes cantidades:
| Trimestre | Unidades |
|---|---|
| Primero | 9000 |
| Segundo | 24000 |
| Tercero | 20000 |
| Cuarto | 7000 |
Planeamiento tiene estimado que cuesta $2/unid. el incremento de producción de un trimestre a otro y $1,5/unid. la disminución de la producción. La demanda de un trimestre puede ser satisfecha con unidades almacenadas en trimestres anteriores. La capacidad de almacenamiento está limitada a 5000 unidades. La producción programada para el cuarto trimestre del corriente año es de 6000 unidades y se debe mantener un nivel de inventarios a fin del año próximo inferior a 1000 unidades.
Se debe definir el programa de producción trimestral que haga mínimo el costo de variaciones del nivel de actividad y que asegure un stock suficiente para satisfacer las cantidades pronosticadas en todos los trimestres.
Establezca todas las hipótesis de trabajo requeridas para una formulación completa del enunciado del problema.
Resolución
El costo de set-up de la producción será de 1$ por unidad en caso de aumento de producción de un trimestre al siguiente, y de 0,5$ en caso de disminución de la misma.
Definición de variables
 :Producción en el trimestre “i”.
:Producción en el trimestre “i”.
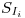 :Stock al inicio del trimestre “i”.
:Stock al inicio del trimestre “i”.
 :Stock al final del trimestre “i”.
:Stock al final del trimestre “i”.
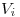 :Ventas en el trimestre “i”.
:Ventas en el trimestre “i”.
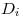 :Demanda en el trimestre “i”.
:Demanda en el trimestre “i”.
 :Variación positiva (aumento) de la producción del trimestre “i-1” al trimestre “i”.
:Variación positiva (aumento) de la producción del trimestre “i-1” al trimestre “i”.
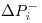 :Variación negativa (disminución) de la producción del trimestre “i-1” al trimestre “i”.
:Variación negativa (disminución) de la producción del trimestre “i-1” al trimestre “i”.
Hipótesis
Todas las variables son enteras y positivas.
 Sin motivo particular el valor 1000, pero hay que tomar algún valor.
Sin motivo particular el valor 1000, pero hay que tomar algún valor.
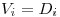 Se desprende del enunciado.
Se desprende del enunciado.
Ecuaciones
Balance de producción: 
Variación de la producción: 
Stocks: 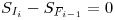
Límite de capacidad de almacén: 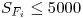
Valores de inicio:\\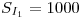

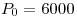
Función Objetivo: Minimizar 
