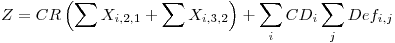Ejercicio de Parcial de Modelización - 71.07. Investigación Operativa
Cátedra: Miranda
Enunciado
Plantear el modelo del problema que se enuncia a continuación, indicando:
- Interrogantes y objetivo
- Hipótesis y supuestos
- Variables, significado y unidades
- Inecuaciones y/o ecuaciones que constituyen el modelo
- Funcional
- Variables slacks, significado y unidades
La fábrica de amoblamientos Woodmakers posee 29 máquinas para producir mesas, sillas y placards. Al iniciar la producción, posee un determinado stock de cada tipo de muebles. Debe cumplir con los siguientes pedidos para los próximos tres días:
| Stock | PEDIDOS | |||
|---|---|---|---|---|
| Inicial | MIERCOLES | JUEVES | VIERNES | |
| Mesas | 20 | 40 | 50 | 20 |
| Sillas | 0 | 10 | 20 | 40 |
| Placards | 15 | 5 | 5 | 25 |
Las máquinas se descalibran con el uso durante el tiempo, y este hecho hace disminuir su rendimiento.
| RENDIMIENTO DIARIO (muebles/día) | |||
|---|---|---|---|
| Primer día | Segundo Día | Tercer día | |
| Mesas | 2,2 | 2 | 1,8 |
| Sillas | 3 | 2,5 | 2 |
| Placards | 2,3 | 2,1 | 1,7 |
El costo de calibrar una máquina es de $100, volviendo la misma a rendir como el primer día. Cuando se deja de cumplir con un pedido se produce una pérdida de 30$/mesa, 40$/silla y 50$/placard.
Resolución
Se debe determinar cuántas máquinas deben producir cada producto cada día, y cuantas deben ser recalibradas cada día. El objetivo es minimizar las pérdidas producidas por penalización del cliente y por recalibración de las máquinas.
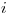 Producto (M;S;P)
Producto (M;S;P)
 Día (1;2;3)
Día (1;2;3)
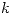 Día de recalibración (1;2)
Día de recalibración (1;2)
 Rendimiento de la Máquina el día
Rendimiento de la Máquina el día  produciendo el producto
produciendo el producto 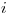
 Cantidad de Máquinas asignadas a producir
Cantidad de Máquinas asignadas a producir 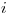 el día
el día  que fueron recalibradas el día
que fueron recalibradas el día 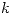
 Costo de recalibrar.
Costo de recalibrar.
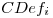 Costo de déficit de producto
Costo de déficit de producto 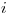
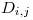 Demanda del producto
Demanda del producto 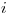 el día
el día 
 Stock al final del día
Stock al final del día  del producto
del producto 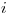
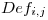 Deficit de producto
Deficit de producto 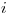 el día
el día  .
.
 Producción de producto
Producción de producto 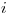 el día
el día  .
.
Producción del primer día: 
Cantidad de máquinas del primer día: 
Producción del segundo día: 
Cantidad de máquinas del segundo día: 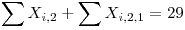
Producción del tercer día: 
Cantidad de máquinas del tercer día: 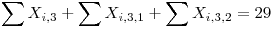
La cantidad de máquinas recalibradas despues del primer día que se usan el tercer día, debe ser menor a la cantidad recalibrada después del primer día: 
Balance de producción, stock, demanda y deficit:

Funcional a Minimizar: