Examen Parcial - 71.07. Investigación Operativa - 08/06/2009

2009

Cátedra: Miranda/02
Fecha: 1° Oportunidad - Primer Cuatrimestre 2009
Día: 08/06/2009

Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
Además, estaría bueno que si hacés alguna corrección vos mismo, la expliques brevemente en la última sección llamada “Discusión - Correcciones”.

Enunciado

Ejercicio de Colas

En una clínica de kinesiología, en donde hay 3 médicos, el sistema de atención es el siguiente:

Cada persona que entra a la clínica pasa directamente a la sala de alguno de los médicos (en caso de que al menos uno esté desocupado).
Si los 3 están ocupados, se sienta a esperar en la sala de recepción, hasta que alguno se libere.
Se estima que, de las personas que al acercarse a la clínica (en promedio se acercan unas 5 personas por hora) ven que hay 1 persona esperando en la sala de recepción, sólo entra la mitad. Si hay 2 personas esperando, no entra nadie más. En caso de no haber personas esperando en la sala, todos ingresan.
Cada sesión dura en promedio unos 30 minutos.
Los clientes no tienen preferencia por ninguno de los 3 médicos.
Toda persona, al terminar con la sesión (independientemente de con cuál de los médicos se haya tratado), debe dirigirse a una única sala en donde se efectúa el pago y llenado de formularios. En esta nueva sala hay un solo empleado, que atiende por orden de llegada a la misma. Esta sala no tiene restricciones de capacidad. El tiempo promedio que tarda este empleado en atender a un cliente es de 10 minutos.
Luego de este trámite, el cliente se retira de la clínica.

Calcular el tiempo total que una persona permanece en la clínica.

Resolución

Lo recomendable para comenzar, a mi criterio, es dividir al sistema en dos subsistemas separados, a saber:

El subsistema 1 tiene una tasa de llegada igual a la de los pacientes a la clínica, el proceso de ingreso y espera descripto en el enunciado, y dos canales de atención, lo que derivará en una tasa de salida promedio que se calculará más adelante.
Por otro lado, el subsistema 2 comienza cuando los pacientes terminan de ser atendidos y se ubican en la cola para el segundo paso, que es el pago del servicio. Posee una tasa de llegada determinada, un canal de atención, no posee restricciones de capacidad, y tendrá una tasa de salida promedio que calcularemos luego.

Como se ve, es importante notar que los dos subsistemas cubren el 100 % del tiempo que los pacientes están dentro del sistema completo. Por lo tanto, podemos asumir que el tiempo promedio total que una persona permanece en la clínica será la suma de los tiempos promedios que los pacientes permanecen en cada uno de los dos subsistemas. Aclarado esto, empezamos a resolver:

Subsistema 1

Tenemos, según los datos del enunciado:

$<tex>\lambda = \left\{ \begin{array}{ll}\lambda & n=0\\\lambda & n=1\\\lambda & n=2\\\lambda & n=3\\\frac{\lambda}{2} & n=4\\0 & n=5\\\end{array} \right.\qquad y\qquad\mu = \left\{ \begin{array}{ll}0 & n=0\\\mu & n=1\\2\mu & n=2\\3\mu & n=3\\3\mu & n=4\\3\mu & n=5\\\end{array} \right.</tex>$

Ahora, cumpliéndose las condiciones necesarias (que ahora no recuerdo como para enumerar) podemos aplicar la Ley de Régimen Permanente:

$<tex>p(n)=p(n-1)\frac{\lambda_{n-1}}{\mu_n} \\</tex>$

Y así obtenemos:
(Recordando que: $<tex>\rho=\frac{\lambda}{\mu}</tex>$ )

$<tex>p(1) = p(0)\frac{\lambda}{\mu}=p(0)\rho \\\\p(2)=p(1)\frac{\lambda}{2\mu}=p(0)\rho\frac{\lambda}{2\mu}=p(0)\frac{\rho^2}{2} \\\\p(3)=p(2)\frac{\lambda}{3\mu}=p(0)\frac{\rho^2}{2}\frac{\lambda}{3\mu}=p(0)\frac{\rho^3}{6} \\\\p(4)=p(3)\frac{\lambda}{3\mu}=p(0)\frac{\rho^3}{6}\frac{\lambda}{3\mu}=p(0)\frac{\rho^4}{18} \\\\p(5)=p(4)\frac{\lambda}{3\mu}=p(0)\frac{\rho^4}{18}\frac{\frac{\lambda}{2}}{3\mu}=p(0)\frac{\rho^5}{108} \\</tex>$

Aquí llegamos a un sistema con 5 ecuaciones y 6 incógnitas; para completar el sistema, nos falta 1 ecuación, que es la siguiente:

$<tex>\sum_{n=0}^{n}p(n)=1 \\\Rightarrow p(0)+p(0)\rho+p(0)\frac{\rho^2}{2}+p(0)\frac{\rho^3}{6}+p(0)\frac{\rho^4}{18}+p(0)\frac{\rho^5}{108}=1 \\\Rightarrow p(0)(1+\rho+\frac{\rho^2}{2}+\frac{\rho^3}{3}+\frac{\rho^4}{4}+\frac{\rho^5}{5})=1 \\\Rightarrow p(0)=0,0813 \\</tex>$
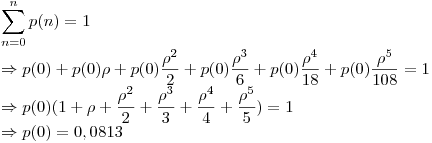
A partir de este valor, calculamos las otras 5 probabilidades, resultando: $<tex>\left\{ \begin{array}{lcr}p(0) & = & 0,0813 \\p(1) & = & 0,2032 \\p(2) & = & 0,2540 \\p(3) & = & 0,2117 \\p(4) & = & 0,1764 \\p(5) & = & 0,0735 \\\end{array} \right.</tex>$

No está de más en este punto hacer algún tipo de comprobación de los cálculos, el primero y más fácil es que la suma de esos valores sea efectivamente 1. Y otro es calcular los valores $<tex>\overline \lambda</tex>$ y $<tex>\overline \mu</tex>$ , que luego necesitaremos, y compararlos. Recordemos cómo hacerlo:

$<tex>\overline \lambda=\lambda - R=\sum_{n=0}^{5}p(n)\lambda_n \\\overline \mu=\sum_{n=0}^{5}p(n)\mu_n \\</tex>$

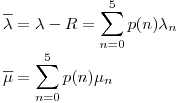
Además, debemos saber que, a menos que los pacientes abandonen el consultorio habiendo ingresado al mismo (cosa que no sucede en este ejercicio), la tasa promedio de ingreso al sistema debe ser igual a la tasa de salida promedio, o tasa de atención promedio. Es decir, para este caso:

$<tex>\overline \lambda=\overline \mu \\ </tex>$
Por lo que no viene mal comprobar que esto se cumpla, es una forma más de ir viendo si cometimos algún error en los cálculos o planteos previos.

Ahora calculamos la longitud promedio de personas dentro del sistema, es decir L:
$<tex>L=\sum_{n=0}^{5}p(n)n=2,4194 \\</tex>$
Ya para terminar la resolución del Subsistema 1, aplicamos una de las denominadas “Fórmulas de Little”:

$<tex>W=\frac{L}{\overline \mu}=\frac{2,4194}{4,192}=0,5771 \;horas=34,6 \; minutos \\</tex>$
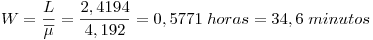
(Llamamos W al tiempo total promedio que permanece una persona en el sistema, es decir desde que ingresa hasta que termina de ser atendido y se retira)

Subsistema 2

Lo primero que hay que hacer es relacionar éste subsistema con el anterior. Creo que no es ninguna revelación decir que, siendo que TODOS los pacientes que terminan de atenderse DEBEN obligatoriamente efectuar el pago del servicio, la tasa promedio de salida / atención ( $<tex>\overline \mu</tex>$ ) del Subs.1 será igual la tasa de llegada ( $<tex>\lambda</tex>$ ) del Subs.2

Por lo tanto 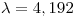$<tex>\lambda=4,192</tex>$

Nuestro único canal de atención tiene una tiempo de servicio de 10 minutos, por lo que:

$<tex>\mu=\frac{1 \;cliente}{10 \;minutos} \frac{60 \;minutos}{hora}=6 \frac{clientes}{hora} </tex>$

Con estos datos sabemos que estamos en presencia de un sistema P/P/1, con: 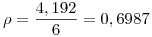$<tex>\rho=\frac{4,192}{6}=0,6987</tex>$ (vemos que es menor a 1, lo que permite la existencia de solución, es decir, evita que la cola crezca infinitamente…)

No me voy a extender demasiado en los cálculos, ya que éstos pueden ser vistos en la teoría, lo resumiré como sigue:

Planteando la Ecuación de régimen permanente para los estandos n=1,2,3,4… podremos ver el comportamiento de p(n). Por lo que luego, con la ecuación extra de que las probabilidades de todos estos estados posibles deben sumar 1 llegamos a lo siguiente:

$<tex>\sum_{n=0}^{\infty}p(n)\rho^n=1=p(0)\sum_{n=0}^{\infty}\rho_n \\\Rightarrow p(0)=\frac{1}{\sum_{n=0}^{\infty}\rho_n} \\\Rightarrow p(0)=1-\rho=0,3013 \\</tex>$

Luego, recordando la fórmula de Little, necesitamos disponer de los valores de L y la tasa promedio de salida.

$<tex>L=\sum_{n=0}^{\infty}p(n)n=\frac{\rho}{1-\rho}=\frac{\frac{0,6987}{1-0,6987}}{4,192}=2,3190 \\ </tex>$
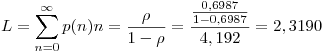
(Nuevamente, no detallo los cálculos, los mismos son resoluciones de series relativamente simples)

En este subsistema, al igual que en el anterior, no existe Abandono, es decir, todas los pacientes que ingresan aguardan a ser atendidos, y luego se retiran, ninguno abandona previo a eso. Por otro lado, tampoco existe rechazo, por lo que TODOS los pacientes que arriban a este subsistema ingresan en él. Por lo tanto, podemos afirmar:

$<tex>\overline \lambda=\lambda-R= \lambda=4,192 \\\overline \mu=\overline \lambda - A = \overline \lambda=4,192 \\</tex>$

Luego: $<tex> W = \frac{L}{\overline \mu}=\frac{2,3190}{4,192}=0,5532 \;horas = 33,2 \;minutos</tex>$

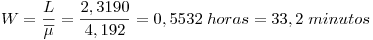
Para finalizar, y como planteamos inicialmente:

$<tex>W_{total}=W_1+W_2=34,6+33,2=67,8 \;minutos=1,13 \;horas</tex>$