Ejercicios Resueltos
En esta página iremos volcando algunos ejercicios, y están invitados a sumar ustedes también.
Modelización
1.7 Taller de tejido de pulloveres
Un taller de tejido de pullovers elabora varios modelos, los que se pueden agrupar desde el punto de vista técnico-económico en tres tipos de prendas diferentes: A, B y C.
El taller posee dos máquinas: I y II. Los pullovers A solo se pueden fábricar en la máquina I, los C en la II y los B en la I o en la II.
Las dos máquinas trabajan 2 turnos de 8 horas de lunes a viernes.
La materia prima utilizada es lana de dos calidades distintas: M se usa para los A y C, y N para los tipo B. De la lana M es posible conseguir hasta 20 kg. por semana y de la N hasta 36 Kg. por semana.
Existe un compromiso con un importante distribuidor de entregar 10 pullovers de tipo B por semana.
El objetivo del problema es maximizar los beneficios.
Los standards de producción, standards de Materia Prima y el beneficio unitario para cada tipo de pullover se dan en el siguiente cuadro:
| Standard de Producción | Standard de MP | Beneficio Unitario | |||
|---|---|---|---|---|---|
| I | II | M | N | ||
| A | 5 | - | 1.6 | - | 50 |
| B | 6 | 4 | - | 1.8 | 70 |
| C | - | 4 | 1.2 | - | 80 |
| Disponibilidad Semanal | 80 | 80 | 20 | 36 | |
Resolución
Antes de plantear la función objetivo, es necesario definir las variables:
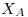 : Cantidad de pulloveres de tipo A a producir,
: Cantidad de pulloveres de tipo A a producir,
 : Cantidad de pulloveres de tipo B a producir en la máquina I (en el desarrollo del problema, se llega a la conclusión que se debe tratar independientemente a los pulloveres B producidos por cada máquina),
: Cantidad de pulloveres de tipo B a producir en la máquina I (en el desarrollo del problema, se llega a la conclusión que se debe tratar independientemente a los pulloveres B producidos por cada máquina),
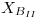 : Cantidad de pulloveres de tipo B a producir en la máquina II,
: Cantidad de pulloveres de tipo B a producir en la máquina II,
 : Cantidad de pulloveres de tipo C a producir.
: Cantidad de pulloveres de tipo C a producir.
De esta forma, la función objetivo queda:
Maximizar 
Sujeto a las siguientes restricciones:
MáquinaI)
 Este ejercicio está incompleto.
Este ejercicio está incompleto.
1.17 Compañía discográfica
La empresa Record-a-Song Company ha contratado a una estrella en ascenso para grabar ocho canciones. La duración de esas canciones es de 8,3,5,5,9,6,7 y 12 minutos, respectivamente.
La compañía utiliza cinta de ida y vuelta para la grabación. Cada lado tiene 30 minutos de capacidad; y desea distribuir las canciones en los dos lados, en forma equilibrada (es decir que la duración en cada lado debe ser más o menos la misma, hasta donde sea posible).
Resolución
Aclaro antes que nada que la idea de resolución de este ejercicio no se me ocurrió a mi, sino que se planteó durante la clase. Yo solamente explico un poco la idea de la solución, e hice una planilla de Excel para mostrar cómo resolverlo con el Solver, complemento que proporciona dicho programa.
Hay que tener en cuenta, en primer lugar, que el objetivo es que los lados terminen con una duración lo más parecida posible, esto se logra pidiendo que la diferencia de duración entre los lados A y B sea MÍNIMA, por lo tanto, este será nuestro funcional.
Llamaremos  a la duración del lado A. y
a la duración del lado A. y  a la duración del lado B.
a la duración del lado B.

Ahora ingresaremos una a una las restricciones:
Este primer conjuto asigna a cada tema ( ) su duración, pero lo hace multiplicando su duración por variables binarias, asignando
) su duración, pero lo hace multiplicando su duración por variables binarias, asignando  para que el tema entre en el lado A y
para que el tema entre en el lado A y  para que el tema entre en lado B.
También fijamos que cada suma
para que el tema entre en lado B.
También fijamos que cada suma 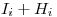 sea obligatoriamente igual a 1 (Esto obliga a que todos los temas estén en el disco, sea en el lado A o en el lado B; y que NO estén en ambos lados!).
sea obligatoriamente igual a 1 (Esto obliga a que todos los temas estén en el disco, sea en el lado A o en el lado B; y que NO estén en ambos lados!).


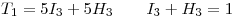
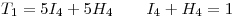

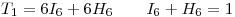
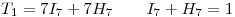

Por último, hay que hacer a las 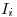 ,
,  Binarias, de modo que sólo pueden valer 0 o 1.
Binarias, de modo que sólo pueden valer 0 o 1.
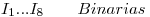

Falta definir, ya que las incluimos en el funcional, las duraciones de ambos lados, a saber:

Simplex
3.4 Refinería de Petróleo
Una refinería de petróleo produce NAFTAS, GASOIL y FUELOIL. La refinería puede funcionar bajo 3 modos diferentes de operación: A, B ó C. La tabla que sigue muestra la cantidad de cada uno de los productos que la refinería es capaz de producir (en miles de barriles/día) bajo cada uno de los regímenes de operación. Se indican además, los márgenes de beneficio de cada uno de los productos en $/bbl.
| Naftas | Gas Oil | Fuel Oil | |
|---|---|---|---|
| A | 14 | 6 | 0 |
| B | 14 | 4 | 2 |
| C | 10 | 6 | 4 |
| Margen | 10 | 5 | -2 |
Se desea programar la operación de la refinería para un mes de 30 días, de modo de hacer máximo el margen de beneficio sabiendo que es necesario abastecer el mercado de FUELOIL que demanda 20 mil barriles/mes, y el de GASOIL que demanda 30 mil barriles/mes. El mercado es capaz de tomar toda la oferta de NAFTAS sin deterioro en el margen. El problema ha sido planteado como uno de Programación Lineal de la siguiente forma:
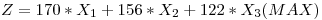



- Describa el programa de producción óptimo. Principales variables y unidades.
- ¿Cuánto GASOIL y FUELOIL se produce por encima del mínimo requerido?
- ¿Cómo variará el funcional si se incrementa en un día la operación tipo C?
- ¿Qué beneficio o pérdida generará la reducción de los requerimientos mínimos de FUELOIL en 1 unidad?
- ¿Qué variación sufriría el beneficio si el mes fuera de 31 días?
- Graficar el valor del funcional, y de la producción de los 3 productos cuando la exigencia de la producción mínima de FUELOIL varía entre 0 y 20 mil barriles/mes.
- ¿Es conveniente la instalación de un nuevo proceso D que es capaz de producir 14 mil barriles/día de NAFTAS, 4 mil de GASOIL y 4 mil de FUELOIL?
Tabla Directa Inicial
| 170 | 156 | 122 | |||||||
| C | X | b | A1 | A2 | A3 | A4 | A5 | A6 | A7 |
|---|---|---|---|---|---|---|---|---|---|
| -10000 | u1 | 30 | 6 | 4 | 6 | -1 | |||
| -10000 | u2 | 20 | 0 | 2 | 4 | -1 | |||
| -10000 | u3 | 30 | 1 | 1 | 1 | -1 | |||
| 0 | x7 | 30 | 1 | 1 | 1 | 1 | |||
| Z=-800000 | -70170 | -70156 | -110122 | 0 | 0 | 0 | 0 | ||
Tabla Óptima Directa
| 170 | 156 | 122 | |||||||
| C | X | b | A1 | A2 | A3 | A4 | A5 | A6 | A7 |
|---|---|---|---|---|---|---|---|---|---|
| 156 | x2 | 10 | 1 | 2 | -0,5 | 0 | |||
| 0 | x4 | 130 | 0 | -4 | 1 | 1 | 6 | ||
| 170 | x1 | 20 | 1 | 0 | -1 | 0,5 | 1 | ||
| 0 | x6 | 0 | 0 | 0 | 0 | 1 | 1 | ||
| Z=4960 | 0 | 0 | 20 | 0 | 7 | 0 | 170 | ||
Tabla Óptima Dual
| -30 | -20 | -30 | 30 | ||||||
| C | X | b | A1 | A2 | A3 | A4 | A5 | A6 | A7 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | y7 | 20 | 4 | 0 | 1 | -2 | 1 | ||
| -20 | y2 | 7 | -1 | 1 | 0 | -0,5 | 0,5 | ||
| 30 | y4 | 170 | -6 | -1 | 1 | -1 | 0 | ||
| Z=4960 | -130 | 0 | 0 | 0 | -20 | -10 | 0 | ||
