Tabla de Contenidos
70.03 Medios de Representación "A" - Trabajo Práctico - Tronco de Cono
Período: 1er Cuatrimestre 2007
Alumno: García Mendive, Iñaki
Lámina
Resolución
- Determinar el área circular que será el desarrollo del cono: Para empezar, el radio de la circunferencia que limita a este área será igual a
 , longitud de las generatrices del cono 1). En cuanto al ángulo
, longitud de las generatrices del cono 1). En cuanto al ángulo  , segundo parámetro que delimita al sector, éste se obtiene por una simple relación de proporcionalidad, o regla de tres simple. En efecto, si la longitud del arco de circunferencia fuera igual a
, segundo parámetro que delimita al sector, éste se obtiene por una simple relación de proporcionalidad, o regla de tres simple. En efecto, si la longitud del arco de circunferencia fuera igual a  , entonces el ángulo de apertura sería
, entonces el ángulo de apertura sería 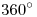 ; como la longitud del arco de circunferencia es igual a
; como la longitud del arco de circunferencia es igual a  (siendo
(siendo  el radio de la base del cono), será
el radio de la base del cono), será  .
. - Determinar puntos de la transformada de la elipse: A los fines de lograr esto es requisito dividir la fracción circular obtenida en ocho sectores iguales, separados uno del otro por segmentos que no son sino las transformadas de las generatrices del cono (que no han cambiado durante el desarrollo, justamente por ser rectas). Marcamos así, en el arco de circunferencia (transformada de la base del cono) los puntos
 . Para encontrar puntos de la transformada de la elipse sección, debemos trasladar la verdadera magnitud de los segmentos
. Para encontrar puntos de la transformada de la elipse sección, debemos trasladar la verdadera magnitud de los segmentos  etcétera a partir de
etcétera a partir de  y sobre las generatrices que correspondan. Verificar que
y sobre las generatrices que correspondan. Verificar que  ,
,  ,
,  .
. - Trazado de tangentes en ciertos puntos de la transformada: Es importante notar que la tangente en
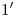 es perpendicular a la generatriz
es perpendicular a la generatriz  , mientras que la tangente en
, mientras que la tangente en  es tangente al arco de circunferencia (transformada de la base del cono) en ése punto. Recordar también que tanto el punto
es tangente al arco de circunferencia (transformada de la base del cono) en ése punto. Recordar también que tanto el punto 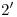 como el
como el 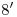 son de infexión de la transformada, como ya se vio en la explicación de la lámina anterior. En cuanto a la tangente en un punto cualquiera de la transformada de la elipse, por ejemplo el
son de infexión de la transformada, como ya se vio en la explicación de la lámina anterior. En cuanto a la tangente en un punto cualquiera de la transformada de la elipse, por ejemplo el 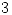 , para hallarla se procede así: trazamos la tangente al arco de circunferencia en
, para hallarla se procede así: trazamos la tangente al arco de circunferencia en 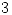 , con una longitud igual a la longitud de
, con una longitud igual a la longitud de 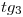 obtenida en la lámina anterior, y al extremo de la misma lo unimos con
obtenida en la lámina anterior, y al extremo de la misma lo unimos con 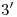 : éste último segmento trazado es la tangente en
: éste último segmento trazado es la tangente en 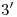 buscada, y el triángulo formado (ver lámina terminada) es el triángulo indeformable en verdadera magnitud.
buscada, y el triángulo formado (ver lámina terminada) es el triángulo indeformable en verdadera magnitud.
Aclaración importante: Nótese que hay un sector circular que ha sido recortado del desarrollo. Su centro es el centro del círculo que contiene al desarrollo, y su radio se obtiene de la lámina anterior, midiendo sobre el contorno aparente ortográfico la distancia desde 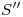 hasta el punto donde dicho contorno corta al del cilindro. Este recorte es consecuencia de la intersección del cono con un cilindro coaxil, siendo el radio del cilindro igual a
hasta el punto donde dicho contorno corta al del cilindro. Este recorte es consecuencia de la intersección del cono con un cilindro coaxil, siendo el radio del cilindro igual a 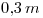 .
.
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
1)
Esta longitud puede ser medida en la lámina precedente, tanto en ortografía como en la proyección auxiliar, sobre el contorno aparente del cono.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported


