Tabla de Contenidos
70.03 Medios de Representación "A" - Trabajo Práctico - Cono de Rotación
Período: 1er Cuatrimestre 2007
Alumno: García Mendive, Iñaki
Lámina
Resolución
- Trazar los contornos aparentes icnográfico y ortográfico del cono: Para el primero, simplemente consiste en dibujar una circunferencia de radio
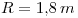 dado, siendo su centro
dado, siendo su centro 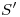 , icnografía del vértice del cono. En cuanto a la ortografía, una vez ubicado
, icnografía del vértice del cono. En cuanto a la ortografía, una vez ubicado 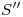 1), se mide a partir de él, y sobre una vertical trazada por él, la altura
1), se mide a partir de él, y sobre una vertical trazada por él, la altura  . Por el punto de la vertical que marca dicha altura se traza una horizontal y se la acota de la siguiente manera: a ambos lados de la misma, y a partir de su intersección con la vertical, se mide el radio
. Por el punto de la vertical que marca dicha altura se traza una horizontal y se la acota de la siguiente manera: a ambos lados de la misma, y a partir de su intersección con la vertical, se mide el radio  dado. Uniéndose los puntos extremos de esta horizontal con
dado. Uniéndose los puntos extremos de esta horizontal con 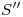 se tiene el contorno aparente ortográfico buscado.
se tiene el contorno aparente ortográfico buscado. - Encontrar las proyecciones horizontal y vertical de las dos rectas
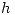 y
y  que determinan al plano sección: Para esto es menester utilizar una proyección auxiliar en la cual el plano sección
que determinan al plano sección: Para esto es menester utilizar una proyección auxiliar en la cual el plano sección 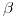 sea proyectante. Por conveniencia, preservaremos la icnografía que ya tenemos y buscaremos una nueva ortografía que cumpla con lo pedido: que la nueva fundamental (que no dibujaremos) sea perpendicular a la icnografía de la horizontal
sea proyectante. Por conveniencia, preservaremos la icnografía que ya tenemos y buscaremos una nueva ortografía que cumpla con lo pedido: que la nueva fundamental (que no dibujaremos) sea perpendicular a la icnografía de la horizontal  y que sea paralela a la icnografía de la recta de máxima pendiente del plano. No tenemos ninguna de éstas dos, pero cabe destacar que a la segunda la podemos elegir siempre y cuando se cumpla que
y que sea paralela a la icnografía de la recta de máxima pendiente del plano. No tenemos ninguna de éstas dos, pero cabe destacar que a la segunda la podemos elegir siempre y cuando se cumpla que  corte al eje del cono, id est que
corte al eje del cono, id est que  .2). Es así que determinamos
.2). Es así que determinamos  3) y sobre una recta que le es perpendicular (que será el eje del cono en esta nueva proyección) marcamos
3) y sobre una recta que le es perpendicular (que será el eje del cono en esta nueva proyección) marcamos 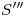 y medimos a partir de éste la altura
y medimos a partir de éste la altura 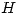 . Cabe notar que si bien la distancia
. Cabe notar que si bien la distancia 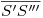 puede ser cualquiera, es conveniente que sea igual a
puede ser cualquiera, es conveniente que sea igual a  pues de esta forma se pueden trasladar puntos de la tercera proyección y viceversa fácilmente utilizando el compás. El contorno aparente del cono en la proyección auxiliar es idéntico al ortográfico (sólo que rotado un cierto ángulo), así que lo dibujamos. Una vez hecho esto, nos posicionamos en alguno de los dos extremos de la terecera proyección de la base del cono, y medimos el ángulo
pues de esta forma se pueden trasladar puntos de la tercera proyección y viceversa fácilmente utilizando el compás. El contorno aparente del cono en la proyección auxiliar es idéntico al ortográfico (sólo que rotado un cierto ángulo), así que lo dibujamos. Una vez hecho esto, nos posicionamos en alguno de los dos extremos de la terecera proyección de la base del cono, y medimos el ángulo  de inclinación del plano (y por ende, de inclinación de
de inclinación del plano (y por ende, de inclinación de  ), o alternativamente marcamos los segmentos de longitudes
), o alternativamente marcamos los segmentos de longitudes 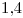 y
y  que también nos dan dicha pendiente (para mayor claridad, ver lámina terminada). Podemos trazar entonces
que también nos dan dicha pendiente (para mayor claridad, ver lámina terminada). Podemos trazar entonces  y determinar los puntos en donde
y determinar los puntos en donde  corta al cono: los trasladamos a la icnografía (
corta al cono: los trasladamos a la icnografía (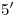 y
y 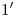 ) y por
) y por 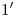 trazamos
trazamos  perpendicular a
perpendicular a  . A
. A 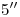 se lo determina fácilmente, subiendo a
se lo determina fácilmente, subiendo a 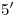 mediante una vertical hasta el contorno aparente ortográfico. Para encontrar
mediante una vertical hasta el contorno aparente ortográfico. Para encontrar 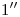 debemos tomar la elevación del mismo (respecto de
debemos tomar la elevación del mismo (respecto de  ) de la proyección auxiliar: por
) de la proyección auxiliar: por  4) trazamos una paralela a
4) trazamos una paralela a  hasta cortar al eje: 5) sobre él podemos medir esta diferencia de elevación, y transportarla al eje en ortografía a partir de
hasta cortar al eje: 5) sobre él podemos medir esta diferencia de elevación, y transportarla al eje en ortografía a partir de 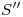 . Por allí trazamos una horizontal, y por
. Por allí trazamos una horizontal, y por 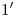 una vertical: donde se corten estará
una vertical: donde se corten estará 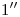 . Alternativamente, si es
. Alternativamente, si es  , se puede proceder así: se traza una vertical por
, se puede proceder así: se traza una vertical por 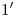 ; se clava el compás en
; se clava el compás en 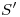 , cuyo extremo se coloca en
, cuyo extremo se coloca en  , y se gira en sentido antihorario hasta cortar a la vertical recién trazada: esa intersección es
, y se gira en sentido antihorario hasta cortar a la vertical recién trazada: esa intersección es 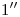 . Ahora, finalmente, se traza
. Ahora, finalmente, se traza 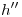 por
por 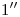 , y
, y 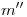 por
por 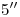 y
y 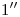 .
. - Trazar la elipse de diámetros principales que es proyección icnográfica de la sección cónica: El diámetro mayor es el
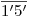 por pertenecer
por pertenecer  a
a  . En cuanto al menor, éste puede ser determinado de la siguiente manera: marquemos el punto medio de
. En cuanto al menor, éste puede ser determinado de la siguiente manera: marquemos el punto medio de 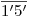 y el de
y el de  (llamémoslos respectivamente
(llamémoslos respectivamente  y
y 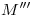 ). Tracemos por
). Tracemos por 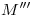 una paralela a la base del cono: en el espacio, ésta será en realidad una circunferencia perteneciente al cono, cuyo centro estará contenido en el eje del mismo. En la proyección auxiliar, la circunferencia ha degenerado en un mero segmento (sobre el cual podemos medir el radio de la misma), pero en icnografía se ve la circunferencia en verdadera magnitud. Podemos trazar entonces en la proyección horizontal una circunferencia con centro en
una paralela a la base del cono: en el espacio, ésta será en realidad una circunferencia perteneciente al cono, cuyo centro estará contenido en el eje del mismo. En la proyección auxiliar, la circunferencia ha degenerado en un mero segmento (sobre el cual podemos medir el radio de la misma), pero en icnografía se ve la circunferencia en verdadera magnitud. Podemos trazar entonces en la proyección horizontal una circunferencia con centro en 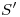 y cuyo radio es la distancia de
y cuyo radio es la distancia de 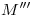 al contorno aparente del cono (medida sobre la paralela a
al contorno aparente del cono (medida sobre la paralela a  trazada por
trazada por 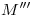 ). Luego, cortamos esta circunferencia con una paralela a
). Luego, cortamos esta circunferencia con una paralela a  trazada por
trazada por  : el segmento de esta paralela que queda así determinado es el diámetro menor de la elipse.
: el segmento de esta paralela que queda así determinado es el diámetro menor de la elipse.
Ahora bien, para encontrar otros puntos de esta elipse podríamos emplear cualquiera de los explicados en esta lámina. Sin embargo, como ejercicio de aplicación de homología, resolveremos la afinidad existente entre la elipse y la circunferencia que es base (y contorno aparente) del cono en icnografía. El centro de homología es impropio (pues se trata de una afinidad) y está en la dirección de . El eje es la intersección entre plano de la base del cono y el plano sección: una paralela a
. El eje es la intersección entre plano de la base del cono y el plano sección: una paralela a  pasante por
pasante por 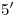 . Pares de puntos correspondientes tenemos dos (aquellos asociados al diámetro mayor):
. Pares de puntos correspondientes tenemos dos (aquellos asociados al diámetro mayor):  y
y  . Para encontrar, por ejemplo, el correspondiente
. Para encontrar, por ejemplo, el correspondiente 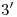 de
de 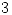 : trazamos
: trazamos  ; luego, unimos
; luego, unimos  con
con 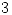 y por donde
y por donde  corta al eje de homología (llamémoslo
corta al eje de homología (llamémoslo 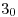 ) trazamos
) trazamos  .
. 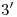 queda determinado por
queda determinado por  . Así podemos proceder para cuantos puntos queramos. En el dibujo he encontrado únicamente
. Así podemos proceder para cuantos puntos queramos. En el dibujo he encontrado únicamente 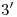 y
y  , y se han encontrado sus simétricos respecto del diámetro menor de la elipse: por ejemplo en el caso de
, y se han encontrado sus simétricos respecto del diámetro menor de la elipse: por ejemplo en el caso de  , se traza por éste una paralela a
, se traza por éste una paralela a  ; clavando el compás en el extremo del diámetro menor y con extremo en
; clavando el compás en el extremo del diámetro menor y con extremo en  se traza un arco de circunferencia. Donde la paralela a
se traza un arco de circunferencia. Donde la paralela a  y el arco se cortan está el simétrico buscado. Otra ventaja de utilizar este método (en lugar de encontrar más puntos por homología) es que se necesitan buscar menos curvas con el pistolete por una cuestión de simetría. Una vez tenidos estos ocho puntos podemos trazar esta elipse. Dada la poca excentricidad de esta elipse debe tenerse cuidado al trazarla para no convertirla involuntariamente en una circunferencia.
y el arco se cortan está el simétrico buscado. Otra ventaja de utilizar este método (en lugar de encontrar más puntos por homología) es que se necesitan buscar menos curvas con el pistolete por una cuestión de simetría. Una vez tenidos estos ocho puntos podemos trazar esta elipse. Dada la poca excentricidad de esta elipse debe tenerse cuidado al trazarla para no convertirla involuntariamente en una circunferencia. - Trazar la elipse de diámetros conjugados que es proyección ortográfica de la sección cónica: El diámetro mayor es el
 . El menor se encuentra trazando una paralela a
. El menor se encuentra trazando una paralela a 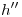 por el punto medio de
por el punto medio de  , y subiendo a ésta los extremos del diámetro menor en icnografía. En el dibujo, se han encontrado cuatro puntos más de esta elipse usando el método de los ocho puntos.
, y subiendo a ésta los extremos del diámetro menor en icnografía. En el dibujo, se han encontrado cuatro puntos más de esta elipse usando el método de los ocho puntos. - Trazados inherentes al desarrollo: para obtener el desarrollo del tronco de cono que es resultado de la sección es necesario tener las verdaderas magnitudes de los segmentos
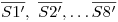 . Para esto haremos uso del giro de las rectas en cuestión. Por ejemplo, en el caso del segmento
. Para esto haremos uso del giro de las rectas en cuestión. Por ejemplo, en el caso del segmento  , tenemos a
, tenemos a  y a
y a 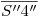 , y en ninguna de estas dos proyecciones apreciamos su verdadera magnitud. Por donde
, y en ninguna de estas dos proyecciones apreciamos su verdadera magnitud. Por donde 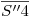 corta a la elipse ortográfica (o sea, por
corta a la elipse ortográfica (o sea, por 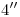 ) trazamos una horizontal hasta intersecar al contorno aparente ortográfico: la distancia desde éste último punto sobre el contorno aparente hasta
) trazamos una horizontal hasta intersecar al contorno aparente ortográfico: la distancia desde éste último punto sobre el contorno aparente hasta 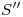 es la distancia buscada. Esto es así porque, si observamos la icnografía, al segmento
es la distancia buscada. Esto es así porque, si observamos la icnografía, al segmento 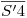 , en definitiva, lo hemos girado hasta colocarlo paralelo a la fundamental (si estuviera dibujada), y en esas condiciones el punto
, en definitiva, lo hemos girado hasta colocarlo paralelo a la fundamental (si estuviera dibujada), y en esas condiciones el punto 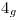 en ortografía se encuentra en el contorno aparente lateral del cono, y entonces también se encuntra allí
en ortografía se encuentra en el contorno aparente lateral del cono, y entonces también se encuntra allí 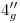 , que es en última instancia el punto que nos interesa. Así se puede proceder para hallar las verdaderas magnitudes de los segmentos restantes. Es importante recalcar que
, que es en última instancia el punto que nos interesa. Así se puede proceder para hallar las verdaderas magnitudes de los segmentos restantes. Es importante recalcar que  ,
,  ,
,  .
.
Ahora vamos a hallar la tangente a los puntos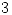 y
y 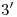 : trazamos
: trazamos 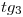 perpendicular al radio de la circunferencia en el punto
perpendicular al radio de la circunferencia en el punto 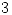 y la prolongamos hasta el eje de homología; desde allí trazamos un segmento hasta
y la prolongamos hasta el eje de homología; desde allí trazamos un segmento hasta 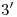 : dicho segmento es
: dicho segmento es  . Ahora tracemos
. Ahora tracemos  . Hemos construido así la icnografía del triángulo indeformable, llamado así por permanecer inmutable durante el desarrollo de la superficie. De esta su proyección nos interesa únicamente el lado
. Hemos construido así la icnografía del triángulo indeformable, llamado así por permanecer inmutable durante el desarrollo de la superficie. De esta su proyección nos interesa únicamente el lado 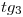 , pues es el único de los tres que se ve en verdadera magnitud. Magnitud que trasladaremos a la lámina del desarrollo para encontrar la tangente a la transformada de la elipse en su punto
, pues es el único de los tres que se ve en verdadera magnitud. Magnitud que trasladaremos a la lámina del desarrollo para encontrar la tangente a la transformada de la elipse en su punto 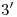 .
.
Lo único que nos resta es encontrar los puntos de la elipse que serán puntos de inflexión de su transformada. ¿Cómo se hace esto? Pues bien, en estos puntos particulares el plano tangente a la superficie que se desarolla (tronco de cono) es perpendicular al plano osculador a la curva que se transforma (elipse). Como esta curva es plana, su plano osculador coincide con el plano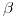 , y entonces el problema en éste caso particular se reduce a hallar dos planos tangentes al cono (hallándose así también dos generatrices de tangencia, y por tanto los dos puntos de la elipse buscados6)), perpendiculares al plano sección. Plano que, como ya vimos, es proyectante en la proyección auxiliar. Comencemos entonces por allí: tracemos una recta
, y entonces el problema en éste caso particular se reduce a hallar dos planos tangentes al cono (hallándose así también dos generatrices de tangencia, y por tanto los dos puntos de la elipse buscados6)), perpendiculares al plano sección. Plano que, como ya vimos, es proyectante en la proyección auxiliar. Comencemos entonces por allí: tracemos una recta  perpendicular al plano, es decir que es
perpendicular al plano, es decir que es  perpendicular a
perpendicular a  , y pasante por
, y pasante por 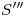 . Esta recta
. Esta recta  será común a los dos planos que hallaremos, y ya nos define la perpendicularidad entre estos dos y el plano sección; sólo resta imponer una condición de tangencia al cono. Para ello, hallaremos la intersección
será común a los dos planos que hallaremos, y ya nos define la perpendicularidad entre estos dos y el plano sección; sólo resta imponer una condición de tangencia al cono. Para ello, hallaremos la intersección  con el plano de la base del cono, en
con el plano de la base del cono, en 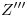 , cuya icnografía
, cuya icnografía 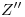 hallamos inmediatamente sobre
hallamos inmediatamente sobre  . Por
. Por 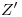 trazamos dos tangentes a la icnografía de la base del cono, que por mera casualidad lo son en
trazamos dos tangentes a la icnografía de la base del cono, que por mera casualidad lo son en 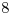 y en
y en  , y por tanto los puntos de inflexión buscados no son sino
, y por tanto los puntos de inflexión buscados no son sino 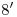 y
y 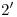 .
.
Aclaración: en la lámina se ve que el vértice del cono no ha quedado intacto, pues el cono ha sido intersecado con un cilindro que le es coaxial (o coaxil), cilindro cuyo radio es igual a 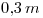 . Esta aclaración no ha sido incluida en los párrafos anteriores para no oscurecer la explicación de los procedimientos más importantes empleados en la resolución de la lámina. Esta intersección hace una pequeña diferencia, sin embargo, a la hora de obtener el desarrollo (más detalles en la explicación de la lámina pertinente).
. Esta aclaración no ha sido incluida en los párrafos anteriores para no oscurecer la explicación de los procedimientos más importantes empleados en la resolución de la lámina. Esta intersección hace una pequeña diferencia, sin embargo, a la hora de obtener el desarrollo (más detalles en la explicación de la lámina pertinente).
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
1)
Sobre la vertical trazada por 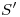 pero con elevación cualquiera.
pero con elevación cualquiera.
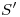 pero con elevación cualquiera.
pero con elevación cualquiera.2)
Tampoco se elige a  recta de perfil ni recta frental, pues en esos casos la ortografía de la tolva no tiene gracia.
recta de perfil ni recta frental, pues en esos casos la ortografía de la tolva no tiene gracia.
 recta de perfil ni recta frental, pues en esos casos la ortografía de la tolva no tiene gracia.
recta de perfil ni recta frental, pues en esos casos la ortografía de la tolva no tiene gracia.3)
Ahora, en base a esta dirección elegida para  , dividiremos la circunferencia (contorno aparente icnográfico) en ocho partes iguales, marcando sobre la misma puntos tales como el
, dividiremos la circunferencia (contorno aparente icnográfico) en ocho partes iguales, marcando sobre la misma puntos tales como el 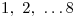 . Luego, subimos cada uno de esos puntos a la ortografía, marcándolos sobre la base del cono.
. Luego, subimos cada uno de esos puntos a la ortografía, marcándolos sobre la base del cono.
 , dividiremos la circunferencia (contorno aparente icnográfico) en ocho partes iguales, marcando sobre la misma puntos tales como el
, dividiremos la circunferencia (contorno aparente icnográfico) en ocho partes iguales, marcando sobre la misma puntos tales como el 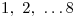 . Luego, subimos cada uno de esos puntos a la ortografía, marcándolos sobre la base del cono.
. Luego, subimos cada uno de esos puntos a la ortografía, marcándolos sobre la base del cono.4)
No nombrado en el dibujo, es el punto que no pertenece a la base del cono y donde  corta al contorno aparente del mismo.
corta al contorno aparente del mismo.
 corta al contorno aparente del mismo.
corta al contorno aparente del mismo.5)
La tercera proyección del eje, en realidad.
6)
Que son intersección de ésta con esas dos generatrices.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported


