Tabla de Contenidos
70.03 Medios de Representación "A" - Trabajo Práctico - Figuras Planas y Cuerpos
Período: 1er Cuatrimestre 2007
Alumno: García Mendive, Iñaki
Lámina
Resolución:
- Encontrar
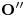 y trazar por él
y trazar por él 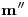 : El ángulo
: El ángulo 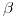 entre el plano del que pende la tuerca y el plano
entre el plano del que pende la tuerca y el plano 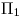 es
es  . Éste ángulo es, también, el que forma
. Éste ángulo es, también, el que forma 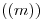 con
con 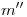 . Trazamos entonces una recta a
. Trazamos entonces una recta a  de ésta última, y luego una paralela a
de ésta última, y luego una paralela a  por
por  . Allí se encontrará
. Allí se encontrará 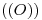 , y la distancia
, y la distancia 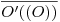 será la altura del punto
será la altura del punto 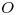 con respecto a
con respecto a 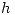 (el eje de abatimiento elegido es
(el eje de abatimiento elegido es  , con lo cual todas las alturas están medidas desde
, con lo cual todas las alturas están medidas desde 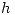 ). Trasladamos esta distancia, sobre una vertical trazada por
). Trasladamos esta distancia, sobre una vertical trazada por  , y a partir de
, y a partir de 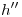 . Hemos encontrado así
. Hemos encontrado así 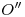 , y tenemos entonces ahora dos puntos conocidos por los que pasa
, y tenemos entonces ahora dos puntos conocidos por los que pasa  :
: 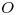 y el punto intersección de
y el punto intersección de  con
con 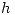 (sabemos que son coplanares, por lo tanto se intersecan). Subiendo la icnografía de este punto de intersección hasta
(sabemos que son coplanares, por lo tanto se intersecan). Subiendo la icnografía de este punto de intersección hasta 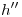 , y uniéndolo con
, y uniéndolo con 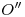 tenemos finalmente
tenemos finalmente 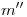 .
. - Obtener el hexágono que es abatimiento de la tuerca sobre el icnográfico: Se continúa el principio de abatimiento que se hizo al obtener
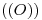 . Para ello se gira con el compás, con centro en la intersección de
. Para ello se gira con el compás, con centro en la intersección de  con
con  y extremo en
y extremo en 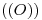 . Sobre la prolongación de
. Sobre la prolongación de  (que es
(que es 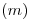 ), en la intersección con el arco recién trazado, se encuentra
), en la intersección con el arco recién trazado, se encuentra 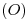 . Con centro en él y radio
. Con centro en él y radio 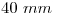 , se traza la circunferencia circunscritora del hexágono. Sobre cualquier punto de la misma (por comodidad, sobre la intersección de ésta con
, se traza la circunferencia circunscritora del hexágono. Sobre cualquier punto de la misma (por comodidad, sobre la intersección de ésta con 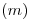 ), se posiciona el compás y se trazan dos segmentos de arco que la corten. Se han encontrado, en este sencillo acto, cuatro vértices del hexágono: el punto de apoyo del compás (
), se posiciona el compás y se trazan dos segmentos de arco que la corten. Se han encontrado, en este sencillo acto, cuatro vértices del hexágono: el punto de apoyo del compás (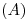 ), el punto diametralmente opuesto a éste (
), el punto diametralmente opuesto a éste ( ), y los dos generados por este último giro del compás (
), y los dos generados por este último giro del compás (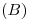 y
y 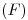 ). Y ahora, como sucederá también más adelante, estamos en una disyuntiva: o bien posicionamos el compás en
). Y ahora, como sucederá también más adelante, estamos en una disyuntiva: o bien posicionamos el compás en  , y obtenemos
, y obtenemos  y
y  mediante un giro (como recién), o bien trazamos por
mediante un giro (como recién), o bien trazamos por 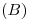 y por
y por 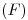 una paralela a
una paralela a 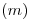 , encontrando en su intersección con la circunferencia a
, encontrando en su intersección con la circunferencia a  y
y  , respectivamente. De una forma u otra, una vez encontrados los seis vértices, se puede trazar el hexágono. Ahora dibujemos la circunferencia interior al mismo, de radio
, respectivamente. De una forma u otra, una vez encontrados los seis vértices, se puede trazar el hexágono. Ahora dibujemos la circunferencia interior al mismo, de radio 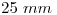 .
. - Obtener la icnografía de la tuerca: Para esto podemos desabatir los seis vértices encontrados uno a uno, o bien podemos sacar provecho de la afinidad (caso particular de homología) existente la icnografía del plano
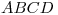 de la tuerca, y su abatimiento. Como no viene nada mal practicarlo, y además es bastante cómodo, aplicaremos este último método. Primero prolongamos las aristas
de la tuerca, y su abatimiento. Como no viene nada mal practicarlo, y además es bastante cómodo, aplicaremos este último método. Primero prolongamos las aristas 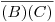 y
y 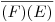 más allá de
más allá de  (obteniéndose los relevamientos1) de estas aristas). Luego unimos
(obteniéndose los relevamientos1) de estas aristas). Luego unimos  con
con 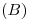 , y prolongamos este segmento hasta que corte al eje de homología (
, y prolongamos este segmento hasta que corte al eje de homología ( ). Allí encontramos
). Allí encontramos 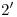 , al cual unimos con
, al cual unimos con  , para, mágicamente,2) hallar
, para, mágicamente,2) hallar 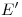 y
y 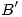 en la intersección de
en la intersección de 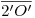 con la prolongación de
con la prolongación de 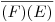 y de
y de 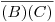 , respectivamente. Luego unimos
, respectivamente. Luego unimos  con
con 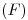 , y prolongamos este segmento hasta que corte al eje de homología (
, y prolongamos este segmento hasta que corte al eje de homología ( ). Allí encontramos
). Allí encontramos 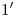 , al cual unimos con
, al cual unimos con  , para hallar
, para hallar 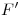 y
y 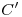 en la intersección de
en la intersección de 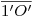 con la prolongación de
con la prolongación de 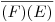 y de
y de 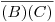 , respectivamente. Para hallar
, respectivamente. Para hallar 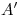 , lo relevamos3): haciendo centro con el compás en la intersección de
, lo relevamos3): haciendo centro con el compás en la intersección de  con
con  y tomando como extremo a
y tomando como extremo a 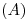 , giramos en sentido antihorario hasta cortar a
, giramos en sentido antihorario hasta cortar a 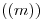 . Por esa intersección trazamos una paralela a
. Por esa intersección trazamos una paralela a  , y donde ella corta a
, y donde ella corta a  tenemos a
tenemos a 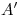 . Para hallar
. Para hallar 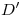 , con centro en
, con centro en  y extremo en
y extremo en 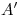 , trazamos un arco que corte a
, trazamos un arco que corte a  . Esta intersección es
. Esta intersección es 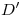 . Uniendo los seis vértices, se puede trazar el hexágono.
. Uniendo los seis vértices, se puede trazar el hexágono.
En cuanto a la elipse, el semidiámetro mayor, paralelo a , se encuentra trazando, justamente, una paralela a
, se encuentra trazando, justamente, una paralela a  por
por  y otra por
y otra por 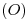 . Por cada uno de los dos puntos donde esta última corta a la circunferencia menor, se traza una paralela a
. Por cada uno de los dos puntos donde esta última corta a la circunferencia menor, se traza una paralela a 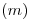 , hasta que corten a la paralela a
, hasta que corten a la paralela a  trazada por
trazada por  . Queda así determinado el semidiámetro mayor. En cuanto al menor, se mide, sobre
. Queda así determinado el semidiámetro mayor. En cuanto al menor, se mide, sobre 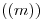 y a partir de
y a partir de 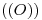 , el radio de la circunferencia menor (
, el radio de la circunferencia menor (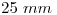 ). Por el punto recién obtenido, se traza una paralela a
). Por el punto recién obtenido, se traza una paralela a  , hasta cortar a
, hasta cortar a  . Sobre
. Sobre  se ha determinado, entonces, un semiradio. El otro semiradio se obtiene trasladando la longitud del susodicho semiradio hacia el otro lado de
se ha determinado, entonces, un semiradio. El otro semiradio se obtiene trasladando la longitud del susodicho semiradio hacia el otro lado de  . En cuanto a la elipse, desde ya que se pueden emplear cualquiera de los métodos explicados para la lámina de Cónicas. Sin embargo, ya que aplicar homología no viene mal para el parcial/final y es muy cómodo, vamos a hacerlo de ese modo. Empecemos trazando una recta horizontal y otra vertical por el centro
. En cuanto a la elipse, desde ya que se pueden emplear cualquiera de los métodos explicados para la lámina de Cónicas. Sin embargo, ya que aplicar homología no viene mal para el parcial/final y es muy cómodo, vamos a hacerlo de ese modo. Empecemos trazando una recta horizontal y otra vertical por el centro 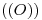 de la circunferencia que es homóloga de la elipse que queremos trazar. Obtenemos entonces cuatro puntos, cuyos correspondientes en la elipse queremos encontrar. Ello se puede hacer (como anteriormente, para los vértices del hexágono), mediante segmentos que unan a dichos puntos con otros ya conocidos, y donde dichos segmentos cortan al eje de homología, trazar los homólogos de estos segmentos, y en la intersección de estos homólogos con perpendiculares a
de la circunferencia que es homóloga de la elipse que queremos trazar. Obtenemos entonces cuatro puntos, cuyos correspondientes en la elipse queremos encontrar. Ello se puede hacer (como anteriormente, para los vértices del hexágono), mediante segmentos que unan a dichos puntos con otros ya conocidos, y donde dichos segmentos cortan al eje de homología, trazar los homólogos de estos segmentos, y en la intersección de estos homólogos con perpendiculares a  , encontrar cuatro puntos de la elipse. Hasta ahora, sin embargo, la homología no parece presentar mucha más comodidad que, por ejemplo, el método de los ocho puntos. Sin embargo, a la hora de encontrar tangentes a los puntos hallados,4) el método es muy sencillo y requiere trazar muy pocas rectas, con lo cual el dibujo no se sobrecarga de líneas. En efecto, como hemos trazado un segmento vertical que corta a la circunferencia, la tangente a dicha circunferencia en los dos puntos hallados es horizontal. En el caso del segmeto vertical, las tangentes a la circunferencia en los otros dos puntos, es vertical. Esas cuatro rectas tangentes deben ser prolongadas, desde la circunferencia hasta el eje de homología, y desde dicho eje hasta el punto que le corresponda a cada una. Podemos trazar así, con gran comodidad, la elipse de diámetros principales de la icnografía de la tuerca.
, encontrar cuatro puntos de la elipse. Hasta ahora, sin embargo, la homología no parece presentar mucha más comodidad que, por ejemplo, el método de los ocho puntos. Sin embargo, a la hora de encontrar tangentes a los puntos hallados,4) el método es muy sencillo y requiere trazar muy pocas rectas, con lo cual el dibujo no se sobrecarga de líneas. En efecto, como hemos trazado un segmento vertical que corta a la circunferencia, la tangente a dicha circunferencia en los dos puntos hallados es horizontal. En el caso del segmeto vertical, las tangentes a la circunferencia en los otros dos puntos, es vertical. Esas cuatro rectas tangentes deben ser prolongadas, desde la circunferencia hasta el eje de homología, y desde dicho eje hasta el punto que le corresponda a cada una. Podemos trazar así, con gran comodidad, la elipse de diámetros principales de la icnografía de la tuerca.
Ahora sólo resta 'dar volumen' a esta figura plana. Para ello, debemos repetir la icnografía ya encontrada, pero desplazada en cierta dirección, y a cierta distancia. ¿Cuál es esa dirección? Bueno, sabemos que la tuerca pende de un cierto plano, dado por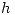 y
y  . También sabemos que la tuerca es recta, o sea, que el ángulo entre el plano de su base y el plano de su lado, es
. También sabemos que la tuerca es recta, o sea, que el ángulo entre el plano de su base y el plano de su lado, es 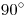 . Entonces, podemos concluir que la dirección en la que debemos 'repetir' la figura plana de la cara de la tuerca, es la dirección normal al plano. En cuanto a la distancia, en los datos figura:
. Entonces, podemos concluir que la dirección en la que debemos 'repetir' la figura plana de la cara de la tuerca, es la dirección normal al plano. En cuanto a la distancia, en los datos figura: 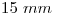 . Sin embargo, la normal al plano pasante por
. Sin embargo, la normal al plano pasante por 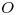 (que en icnografía coincide con
(que en icnografía coincide con  ) no está en verdadera magnitud. Deberíamos entonces abatirla, o girarla, o cambiar de planos, pero no lo haremos. No la abatiremos, porque a los fines prácticos, ya la tenemos abatida: es lo mismo medir distancias sobre
) no está en verdadera magnitud. Deberíamos entonces abatirla, o girarla, o cambiar de planos, pero no lo haremos. No la abatiremos, porque a los fines prácticos, ya la tenemos abatida: es lo mismo medir distancias sobre 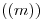 que hacerlo sobre
que hacerlo sobre 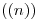 , pues el ángulo entre ellas es
, pues el ángulo entre ellas es 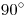 y los puntos se abaten y se relevan en una dirección que es bisectriz de dicho ángulo, en una dirección paralela a
y los puntos se abaten y se relevan en una dirección que es bisectriz de dicho ángulo, en una dirección paralela a  . Medimos, entonces, los
. Medimos, entonces, los 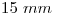 sobre
sobre 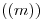 : y resulta que dicho segmento ya está determinado: es el segmento que ha quedado luego de, primero, relevar
: y resulta que dicho segmento ya está determinado: es el segmento que ha quedado luego de, primero, relevar 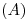 , y segundo, medir
, y segundo, medir 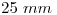 (medida del semiradio menor).5). Ahora que hemos encontrado la distancia en verdadera magnitud, la llevamos a su magnitud aparente en icnografía, trasladamos esta última distancia, en la dirección de
(medida del semiradio menor).5). Ahora que hemos encontrado la distancia en verdadera magnitud, la llevamos a su magnitud aparente en icnografía, trasladamos esta última distancia, en la dirección de 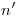 (que es la misma que la de
(que es la misma que la de  ), y alejándonos de
), y alejándonos de  6). La trasladamos a los vértices
6). La trasladamos a los vértices 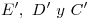 , y a todos los (cuatro) puntos de la elipse que se encuentran entre
, y a todos los (cuatro) puntos de la elipse que se encuentran entre  y la paralela a
y la paralela a  trazada por
trazada por  . Unimos los nuevos vértices encontrados,
. Unimos los nuevos vértices encontrados, 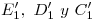 mediante segmentos, y por los cuatro puntos trasladados de la nueva semielipse, trazamos las curvas pertinentes pero sólo hasta su intersección con la elipse primera. Luego de un extenso proeso, hemos completado la icnografía de la tuerca.
mediante segmentos, y por los cuatro puntos trasladados de la nueva semielipse, trazamos las curvas pertinentes pero sólo hasta su intersección con la elipse primera. Luego de un extenso proeso, hemos completado la icnografía de la tuerca. - Obtener la ortografía de la tuerca: En esta última parte (que, no se asuste lector, no será tan larga como la anterior), simplemente subiremos los puntos ya hallados en icnografía, con ayuda de la ortografía de rectas cuya traza sobre
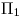 ya tenemos. No es tan complicado como suena (esperemos). Para empezar, tenemos dos rectas, paralelas a
ya tenemos. No es tan complicado como suena (esperemos). Para empezar, tenemos dos rectas, paralelas a  , que contienen, la primera a
, que contienen, la primera a 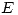 y a
y a  , y la segunda a
, y la segunda a  y
y  . De estas dos rectas, tenemos su icnografía, y encontrar su ortografía no debe ser muy difícil, ya que si son, como suponemos, paralelas a
. De estas dos rectas, tenemos su icnografía, y encontrar su ortografía no debe ser muy difícil, ya que si son, como suponemos, paralelas a  7), sus ortografías deben serlo a
7), sus ortografías deben serlo a 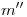 . Necesitamos, además de esto, un punto por el cual trazar estas ortografías. Pues bien, si subimos las intersecciones con
. Necesitamos, además de esto, un punto por el cual trazar estas ortografías. Pues bien, si subimos las intersecciones con  de la icnografía (que ya tenemos) de cada una de estas dos rectas, a
de la icnografía (que ya tenemos) de cada una de estas dos rectas, a 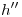 , estará solucionado el problema. Ahora que tenemos entonces estas tres rectas paralelas en icnografía, podemos (ya podíamos antes, en realidad, bastaba tener
, estará solucionado el problema. Ahora que tenemos entonces estas tres rectas paralelas en icnografía, podemos (ya podíamos antes, en realidad, bastaba tener 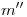 ) subir
) subir 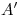 y
y 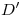 , y (cosa que antes no podíamos) también
, y (cosa que antes no podíamos) también  . Con celeridad hemos obtenido pues la cara de la tuerca. En cuanto a la elipse de diámetros conjugados que tendrá como centro a
. Con celeridad hemos obtenido pues la cara de la tuerca. En cuanto a la elipse de diámetros conjugados que tendrá como centro a 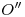 , un semidiámetro puede ser subido a
, un semidiámetro puede ser subido a 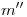 desde su correspondiente sobre
desde su correspondiente sobre  , y el otro puede ser subido a una paralela a
, y el otro puede ser subido a una paralela a 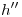 pasante por
pasante por 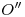 , desde una paralela a
, desde una paralela a  pasante por
pasante por  . . Y en este caso, para encontrar cuatro puntos más de esta elipse, empleamos el método de los ocho puntos.
. . Y en este caso, para encontrar cuatro puntos más de esta elipse, empleamos el método de los ocho puntos.
Ahora, finalmente, para 'dar volumen' a la ortografía de la tuerca, debemos trasladar una cierta distancia en la dirección de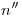 . Dicha distancia puede ser obtenida subiendo el segmento ya encontrado para la icnografía (que se encuentra sobre
. Dicha distancia puede ser obtenida subiendo el segmento ya encontrado para la icnografía (que se encuentra sobre  ), o, lo que es lo mismo, trazando una paralela a
), o, lo que es lo mismo, trazando una paralela a 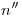 por
por 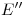 , y subiendo sobre ella
, y subiendo sobre ella 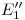 , desde
, desde  . El lector se preguntará: ¿cuál es la dirección de
. El lector se preguntará: ¿cuál es la dirección de 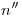 ? Pues bien, es perpendicular a la ortografía de una frental cualquiera del plano. En este caso, hemos tomado una frental
? Pues bien, es perpendicular a la ortografía de una frental cualquiera del plano. En este caso, hemos tomado una frental  , cuya icnografía (para no agregar líneas innecesariamente) hemos hecho coincidir con la ortografía de
, cuya icnografía (para no agregar líneas innecesariamente) hemos hecho coincidir con la ortografía de 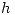 , y cuya ortografía se determina con los siguientes dos puntos: la intersección de
, y cuya ortografía se determina con los siguientes dos puntos: la intersección de  con
con 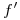 (que coincide con la intersección de
(que coincide con la intersección de 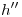 con
con 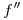 ), y la intersección de
), y la intersección de 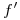 con la paralela
con la paralela  que pasa por
que pasa por 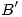 y por
y por 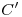 . Así entonces, encontramos esa distancia en la dirección normal, proyección sobre
. Así entonces, encontramos esa distancia en la dirección normal, proyección sobre 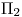 de la distancia verdadera de
de la distancia verdadera de 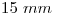 , y la trasladamos a: los puntos
, y la trasladamos a: los puntos  ,8) y los puntos de la elipse que se encuentran entre la diagonal más parecida al segmento
,8) y los puntos de la elipse que se encuentran entre la diagonal más parecida al segmento  y
y 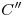 . A los puntos
. A los puntos  los unimos mediante segmentos. A los puntos obtenidos de la nueva semielipse, mediante arcos elípticos (iguales a los arcos correspondientes de la elipse anterior), pero sólo hasta su intersección con los arcos de la elipse anterior. Hemos completado finalmente la ortografía de la tuerca, y con ello, la lámina.
los unimos mediante segmentos. A los puntos obtenidos de la nueva semielipse, mediante arcos elípticos (iguales a los arcos correspondientes de la elipse anterior), pero sólo hasta su intersección con los arcos de la elipse anterior. Hemos completado finalmente la ortografía de la tuerca, y con ello, la lámina.
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
1)
relevamiento: procedimiento inverso al abatimiento
2)
Sande dixit
3)
también lo podríamos haber hecho por homología, utilizando segmentos como veníamos haciendo hasta ahora
4)
Siendo las tangentes muy convenientes a la hora de trazar curvas con el pistolete
5)
El hecho de que ese segmento haya quedado de 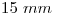 depende única y exclusivamente de la distancia de
depende única y exclusivamente de la distancia de 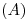 a
a  , la cual es totalmente arbitraria, pues depende, en definitiva, de la distancia de
, la cual es totalmente arbitraria, pues depende, en definitiva, de la distancia de  a
a 
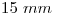 depende única y exclusivamente de la distancia de
depende única y exclusivamente de la distancia de 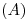 a
a  , la cual es totalmente arbitraria, pues depende, en definitiva, de la distancia de
, la cual es totalmente arbitraria, pues depende, en definitiva, de la distancia de  a
a 
6)
nos alejamos de  pues la tuerca pende del plano
pues la tuerca pende del plano
 pues la tuerca pende del plano
pues la tuerca pende del plano7)
lo suponemos pues forman parte, junto con  , del plano de la cara de la tuerca
, del plano de la cara de la tuerca
 , del plano de la cara de la tuerca
, del plano de la cara de la tuerca8)
El 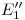 ya lo habíamos obtenido
ya lo habíamos obtenido
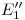 ya lo habíamos obtenido
ya lo habíamos obtenidoExcepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported


