Tabla de Contenidos
70.03 Medios de Representación "A" - Trabajo Práctico - Problemas de Magnitud
Período: 1er Cuatrimestre 2007
Alumno: García Mendive, Iñaki
Lámina
Resolución
- Hallar la icnografía de la cubierta: Para ello, empecemos por trazar la icnografía de la base, tal como nos indican (dos puntos de la misma deben estar contenidos en una recta paralela a la fundamental). Una vez hecho esto, dibujemos las alturas de este triángulo de la base: donde se corten estará
 . Ahora vemos, sin embargo, que no podemos completar la icnografía tan simplemente, pues no conocemos las distancias
. Ahora vemos, sin embargo, que no podemos completar la icnografía tan simplemente, pues no conocemos las distancias 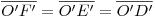 . Debemos recurrir, pues, a una proyección auxiliar: imaginemos que seccionamos a la cubierta laminar con un plano vertical, según los segmentos
. Debemos recurrir, pues, a una proyección auxiliar: imaginemos que seccionamos a la cubierta laminar con un plano vertical, según los segmentos 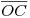 y
y 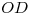 . Imaginemos que de las dos partes de la cubierta, nos quedamos con la que contiene a los puntos
. Imaginemos que de las dos partes de la cubierta, nos quedamos con la que contiene a los puntos 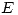 y
y  (que en icnografía, sería la mitad de la derecha), y proyectémosla desde un punto impropio en la dirección
(que en icnografía, sería la mitad de la derecha), y proyectémosla desde un punto impropio en la dirección 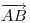 sobre un plano perpendicular a la fundamental1). En primer lugar, veamos que tanto
sobre un plano perpendicular a la fundamental1). En primer lugar, veamos que tanto 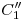 como
como  se localizan sobre la nueva fundamental
se localizan sobre la nueva fundamental ![<tex>[1]</tex> <tex>[1]</tex>](lib/plugins/latex/images/399caa8c0f48360e6df32933586bae3db2928ada_0.png) en una paralela a
en una paralela a 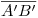 trazada por los puntos en cuestión. Por otro lado, notamos que, en esta nueva ortografía, veríamos a los segmentos
trazada por los puntos en cuestión. Por otro lado, notamos que, en esta nueva ortografía, veríamos a los segmentos 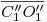 y
y 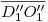 en verdadera magnitud. Pero entonces no es difícil encontrar
en verdadera magnitud. Pero entonces no es difícil encontrar 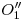 : tomamos la distancia
: tomamos la distancia 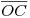 de la hoja de datos, que será el radio de un arco de circunferencia que trazaremos con centro en
de la hoja de datos, que será el radio de un arco de circunferencia que trazaremos con centro en 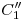 . Donde este arco corte a la perpendicular a
. Donde este arco corte a la perpendicular a ![<tex>[1]</tex> <tex>[1]</tex>](lib/plugins/latex/images/399caa8c0f48360e6df32933586bae3db2928ada_0.png) trazada por
trazada por  estará
estará 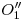 . Para encontrar
. Para encontrar 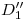 trazamos, con centro en
trazamos, con centro en 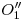 un arco de circunferencia de radio
un arco de circunferencia de radio 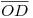 (que también obtenemos de la hoja de datos). Observemos ahora, que el ángulo
(que también obtenemos de la hoja de datos). Observemos ahora, que el ángulo  (o
(o  , para el caso es lo mismo) es recto, y que así se verá en la nueva ortografía: porque
, para el caso es lo mismo) es recto, y que así se verá en la nueva ortografía: porque 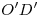 es paralela a
es paralela a ![<tex>[1]</tex> <tex>[1]</tex>](lib/plugins/latex/images/399caa8c0f48360e6df32933586bae3db2928ada_0.png) (es frental para la nueva ortografía) y
(es frental para la nueva ortografía) y 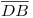 no es perpendicular al plano de proyección auxiliar (o sea, no es perpendicular a la fundamental original)2). En síntesis, sabemos la longitud de
no es perpendicular al plano de proyección auxiliar (o sea, no es perpendicular a la fundamental original)2). En síntesis, sabemos la longitud de 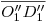 y que
y que 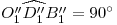 . Esto es suficiente para determinar a
. Esto es suficiente para determinar a 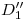 : trazamos el segmento
: trazamos el segmento 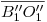 y por su punto medio dibujamos una semicircunferencia de radio
y por su punto medio dibujamos una semicircunferencia de radio 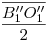 . Donde esta corte al arco antes trazado, estará
. Donde esta corte al arco antes trazado, estará 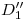 , y uniéndolo con
, y uniéndolo con 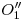 y con
y con  vemos que efectivamente el susodicho ángulo es recto3). Ahora, finalmente, podemos completar la icnografía de la cubierta laminar, trazando por el
vemos que efectivamente el susodicho ángulo es recto3). Ahora, finalmente, podemos completar la icnografía de la cubierta laminar, trazando por el 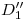 recién encontrado una perpendicular a
recién encontrado una perpendicular a ![<tex>[1]</tex> <tex>[1]</tex>](lib/plugins/latex/images/399caa8c0f48360e6df32933586bae3db2928ada_0.png) hasta cortar a
hasta cortar a 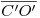 . Tracemos ahora, para terminar, una circunferencia de centro
. Tracemos ahora, para terminar, una circunferencia de centro  y radio
y radio 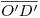 : donde ésta corte a la prolongación de
: donde ésta corte a la prolongación de 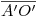 tendremos a
tendremos a 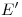 , y donde corte a la prolongación de
, y donde corte a la prolongación de 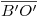 tendremos a
tendremos a 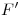 (para que esto último qeude más claro, ver lámina). Notar que tanto
(para que esto último qeude más claro, ver lámina). Notar que tanto 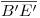 como
como 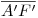 no son perpendiculares a la fundamental original (o lo que es lo mismo, no son paralelos a
no son perpendiculares a la fundamental original (o lo que es lo mismo, no son paralelos a ![<tex>[1]</tex> <tex>[1]</tex>](lib/plugins/latex/images/399caa8c0f48360e6df32933586bae3db2928ada_0.png) ). Para terminar la proyección auxiliar, encontremos
). Para terminar la proyección auxiliar, encontremos  : trazamos una perpendicular a
: trazamos una perpendicular a ![<tex>[1]</tex> <tex>[1]</tex>](lib/plugins/latex/images/399caa8c0f48360e6df32933586bae3db2928ada_0.png) por
por 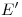 ó por
ó por 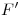 y la cortamos con una paralela a
y la cortamos con una paralela a ![<tex>[1]</tex> <tex>[1]</tex>](lib/plugins/latex/images/399caa8c0f48360e6df32933586bae3db2928ada_0.png) trazada por
trazada por 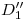 . Estos dos puntos coincidentes nos serán útiles para encontrar
. Estos dos puntos coincidentes nos serán útiles para encontrar  .
. - Hallar la ortografía de la cubierta: Como primer paso, localicemos la ortografía de los puntos
 ,
,  y
y  trazando por
trazando por 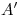 ,
, 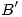 y
y 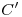 perpendiculares a la fundamental hasta cortarla: allí se localizan respectivamente
perpendiculares a la fundamental hasta cortarla: allí se localizan respectivamente 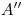 ,
, 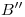 y
y 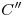 . En cuanto a
. En cuanto a 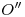 , éste se halla sobre una perpendicular a la fundmaental trazada por
, éste se halla sobre una perpendicular a la fundmaental trazada por  , siendo la elevación de
, siendo la elevación de 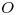 la distancia de
la distancia de 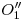 a
a ![<tex>[1]</tex> <tex>[1]</tex>](lib/plugins/latex/images/399caa8c0f48360e6df32933586bae3db2928ada_0.png) .
. 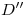 se localiza sobre la misma perpendicular que
se localiza sobre la misma perpendicular que 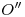 , y su distancia a la fundamental es la distancia de
, y su distancia a la fundamental es la distancia de 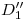 a
a ![<tex>[1]</tex> <tex>[1]</tex>](lib/plugins/latex/images/399caa8c0f48360e6df32933586bae3db2928ada_0.png) . Como
. Como  y
y 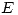 tienen la misma elevación que
tienen la misma elevación que  , si por
, si por 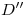 trazamos una paralela a la fundamental y la cortamos con perpendiculares a la misma trazadas por
trazamos una paralela a la fundamental y la cortamos con perpendiculares a la misma trazadas por 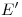 y por
y por 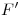 obtenemos respectivamente a
obtenemos respectivamente a 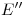 y a
y a 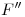 .
. - Hallar la tercera proyección de la cubierta: Para esto, tracemos por
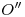 ,
, 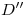 ,
, 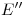 y por
y por 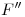 paralelas a la fundamental (las últimas tres son coincidentes entre sí). Ahora, tracemos también paralelas a la fundamental por
paralelas a la fundamental (las últimas tres son coincidentes entre sí). Ahora, tracemos también paralelas a la fundamental por  ,
, 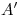 ,
, 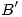 ,
, 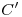 ,
, 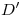 ,
, 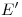 y
y 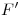 hasta cortar a
hasta cortar a ![<tex>[1]</tex> <tex>[1]</tex>](lib/plugins/latex/images/399caa8c0f48360e6df32933586bae3db2928ada_0.png) , y con centro en
, y con centro en 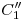 4) y extremo en cada una de esas intersecciones, trazamos un cuarto de circunferencia en sentido antihorario, para trasladar esas intersecciones a la línea de tierra original. Por los puntos que correspondan a
4) y extremo en cada una de esas intersecciones, trazamos un cuarto de circunferencia en sentido antihorario, para trasladar esas intersecciones a la línea de tierra original. Por los puntos que correspondan a 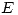 , a
, a  y a
y a  levantamos verticales que corten a la paralela a la fundamental trazada por
levantamos verticales que corten a la paralela a la fundamental trazada por 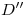 , para encontrar allí a
, para encontrar allí a  . Por el punto correspondiente a
. Por el punto correspondiente a 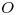 levantamos una vertical hasta cortar a la paralela a la fundamental trazada por
levantamos una vertical hasta cortar a la paralela a la fundamental trazada por 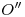 , para encontrar a
, para encontrar a 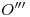 .
.  y
y  se encuentran sobre la fundamental.
se encuentran sobre la fundamental. - Hallar el ángulo
 entre planos
entre planos 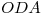 y
y 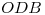 : Resolver este ítem no es tan difícil como quizás parezca a primera vista. Basta darse cuenta que
: Resolver este ítem no es tan difícil como quizás parezca a primera vista. Basta darse cuenta que 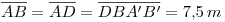 , o sea que el triángulo
, o sea que el triángulo 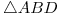 es idéntico al triángulo
es idéntico al triángulo 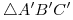 que es la base de la cubierta laminar. Y como el ángulo
que es la base de la cubierta laminar. Y como el ángulo  buscado es, en definitiva, el formado por
buscado es, en definitiva, el formado por 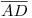 y
y 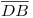 5),
5),  es también el ángulo
es también el ángulo 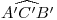 .
. - Hallar el ángulo
 entre planos
entre planos 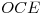 y
y 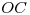 : Para encontrar este ángulo, similarmente a lo hecho en el segundo ítem de ésta lámina, vamos a hacer un cambio de plano de proyección hasta tener a la recta
: Para encontrar este ángulo, similarmente a lo hecho en el segundo ítem de ésta lámina, vamos a hacer un cambio de plano de proyección hasta tener a la recta  (intersección de los dos planos) perpendicular al icnográfico. Primero, notemos que en el cambio de planos ya hecho para el primer ítem, la antedicha recta está en posición frental, con lo cual sólo nos resta la mitad del trabajo: lograr posicionarla como recta de punta. Para ello elegimos una fundamental
(intersección de los dos planos) perpendicular al icnográfico. Primero, notemos que en el cambio de planos ya hecho para el primer ítem, la antedicha recta está en posición frental, con lo cual sólo nos resta la mitad del trabajo: lograr posicionarla como recta de punta. Para ello elegimos una fundamental ![<tex>[2]</tex> <tex>[2]</tex>](lib/plugins/latex/images/f3cafde09b0e97fad8b3c6d9916b90bc5c7c8196_0.png) perpendicular a
perpendicular a 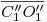 . Seguidamente, sobre una prolongación de
. Seguidamente, sobre una prolongación de 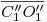 y a partir de
y a partir de ![<tex>[2]</tex> <tex>[2]</tex>](lib/plugins/latex/images/f3cafde09b0e97fad8b3c6d9916b90bc5c7c8196_0.png) llevamos la distancia de
llevamos la distancia de  a
a ![<tex>[1]</tex> <tex>[1]</tex>](lib/plugins/latex/images/399caa8c0f48360e6df32933586bae3db2928ada_0.png) (que es igual a la distancia de
(que es igual a la distancia de 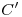 a [1]), encontrando con esto a
a [1]), encontrando con esto a  . Para localizar a
. Para localizar a 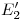 y a
y a 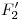 se procede de forma similar: se traza por
se procede de forma similar: se traza por  una paralela a
una paralela a 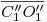 , y a partir de
, y a partir de ![<tex>[2]</tex> <tex>[2]</tex>](lib/plugins/latex/images/f3cafde09b0e97fad8b3c6d9916b90bc5c7c8196_0.png) se miden respectivamente la distancia de
se miden respectivamente la distancia de 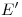 a
a ![<tex>[1]</tex> <tex>[1]</tex>](lib/plugins/latex/images/399caa8c0f48360e6df32933586bae3db2928ada_0.png) y de
y de 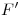 a
a ![<tex>[1]</tex> <tex>[1]</tex>](lib/plugins/latex/images/399caa8c0f48360e6df32933586bae3db2928ada_0.png) .
.  es el ángulo que forman
es el ángulo que forman 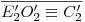 y
y  .
.
En cuanto a la visibilidad en cada una de las proyecciones, ésta se puede obtener mediante el método de los puntos dobles, explicado detalladamente para esta lámina, y ejemplificado sucintamente en el tercer ítem de esta otra lámina.
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
1)
Para entender mejor la operatoria mencionada, así como la que sigue, ver el trazado auxiliar a la derecha de la icnografía en la lámina terminada.
2)
Para más detalles sobre la proyección ortogonal de un ángulo recto, ver: di Lorenzo, Eduardo Oscar, Geometría Descriptiva, tomo I, página 61 (parágrafo 29).
4)
donde se cortan la fundamental original y ![<tex>[1]</tex> <tex>[1]</tex>](lib/plugins/latex/images/399caa8c0f48360e6df32933586bae3db2928ada_0.png) .
.
![<tex>[1]</tex> <tex>[1]</tex>](lib/plugins/latex/images/399caa8c0f48360e6df32933586bae3db2928ada_0.png) .
.5)
Por ser 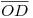 (recta de intersección de los dos planos) perpendicular a ambas.
(recta de intersección de los dos planos) perpendicular a ambas.
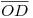 (recta de intersección de los dos planos) perpendicular a ambas.
(recta de intersección de los dos planos) perpendicular a ambas.Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported

