Tabla de Contenidos
70.03 Medios de Representación "A" - Trabajo Práctico - Problemas de Magnitud
Período: 1er Cuatrimestre 2007
Alumno: García Mendive, Iñaki
Lámina
Resolución
- Hallar el ángulo
 entre
entre 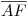 y
y  : Para esto abatiremos el plano formado por estas dos rectas, siendo el eje
: Para esto abatiremos el plano formado por estas dos rectas, siendo el eje 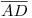 . Para ello trazamos por
. Para ello trazamos por 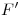 una paralela al mismo, y sobre ella llevamos la elevación del punto
una paralela al mismo, y sobre ella llevamos la elevación del punto  (encontrando así a
(encontrando así a 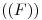 ). Por
). Por 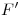 también trazamos una perpendicular al eje (donde se cortan encontramos a
también trazamos una perpendicular al eje (donde se cortan encontramos a 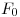 , no notado en el dibujo). Con centro en
, no notado en el dibujo). Con centro en 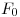 y radio
y radio 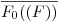 trazamos un arco de circunferencia en sentido antihorario hasta cortar a
trazamos un arco de circunferencia en sentido antihorario hasta cortar a 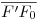 : allí encontramos
: allí encontramos 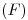 . Uniéndolo con
. Uniéndolo con 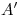 y con
y con 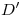 obtenemos los abatimientos de cada una de las dos rectas dadas: el ángulo que forman es el
obtenemos los abatimientos de cada una de las dos rectas dadas: el ángulo que forman es el  buscado.
buscado. - Hallar el ángulo
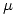 entre dos planos
entre dos planos 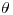 y
y 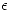 siendo
siendo 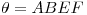 y
y 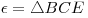 : Para encontrar a
: Para encontrar a 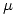 llevaremos a ambos planos a posición proyectante (en este caso sobre el icnográfico) mediante cambios de los planos de proyección. Pero ¿cómo se llevarlos a esa posición? Pues bien, la recta de intersección de ambos planos (
llevaremos a ambos planos a posición proyectante (en este caso sobre el icnográfico) mediante cambios de los planos de proyección. Pero ¿cómo se llevarlos a esa posición? Pues bien, la recta de intersección de ambos planos (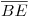 ) debe quedar como recta de punta. Este ejercicio resulta entonces muy similar al último de ésta lámina. Primero debemos, pues llevar a
) debe quedar como recta de punta. Este ejercicio resulta entonces muy similar al último de ésta lámina. Primero debemos, pues llevar a 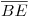 a posición frental: dibujamos entonces la primera nueva fundamental (llamémosla
a posición frental: dibujamos entonces la primera nueva fundamental (llamémosla ![<tex>[1]</tex> <tex>[1]</tex>](lib/plugins/latex/images/399caa8c0f48360e6df32933586bae3db2928ada_0.png) ) paralela a
) paralela a 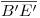 , y pasante (por razones de comodidad) por
, y pasante (por razones de comodidad) por 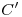 1). Ahora ha lugar una aclaración importante: para no sobrecargar de líneas el dibujo, las nuevas proyecciones que se dibujen, lo serán sólo del techo del galpón (es decir, no se dibujarán las paredes del mismo, pues además no están involucradas en la resolución del problema)2). Siguiendo los pasos indicados para el ejercicio de la lámina ya mencionada, se puede encontrar la nueva ortografía de todos los puntos del techo. Finalmente, para obtener a
1). Ahora ha lugar una aclaración importante: para no sobrecargar de líneas el dibujo, las nuevas proyecciones que se dibujen, lo serán sólo del techo del galpón (es decir, no se dibujarán las paredes del mismo, pues además no están involucradas en la resolución del problema)2). Siguiendo los pasos indicados para el ejercicio de la lámina ya mencionada, se puede encontrar la nueva ortografía de todos los puntos del techo. Finalmente, para obtener a 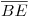 perpendicular al icnográfico, debemos construir nuestra segunda nueva fundamental (
perpendicular al icnográfico, debemos construir nuestra segunda nueva fundamental (![<tex>[2]</tex> <tex>[2]</tex>](lib/plugins/latex/images/f3cafde09b0e97fad8b3c6d9916b90bc5c7c8196_0.png) )3) perpendicular a
)3) perpendicular a 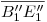 . Con el consabido procedimiento se encuentra la icnografía definitiva de los puntos del techo. Prestar especial atención al hecho de que
. Con el consabido procedimiento se encuentra la icnografía definitiva de los puntos del techo. Prestar especial atención al hecho de que  ,
, 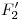 y
y 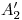 deben estar alineados. También debe ser
deben estar alineados. También debe ser 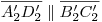 , así como
, así como 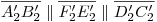 , por ser esto así en las dos proyecciones originales (y por ende en el espacio). Más allá de esto, el ángulo buscado
, por ser esto así en las dos proyecciones originales (y por ende en el espacio). Más allá de esto, el ángulo buscado 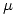 es entre
es entre 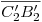 y
y  .
. - Hallar la distancia
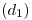 entre la recta
entre la recta 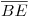 y el punto
y el punto  : Afortunadamente, este ejercicio ya lo hemos resuelto conjuntamente con el anterior: al estar la recta
: Afortunadamente, este ejercicio ya lo hemos resuelto conjuntamente con el anterior: al estar la recta 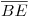 en posición de punta, la distancia que necesitábamos coincide simplemente con el segmento
en posición de punta, la distancia que necesitábamos coincide simplemente con el segmento  .
. - Hallar la distancia
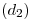 entre el punto
entre el punto  y el plano
y el plano  : Si miramos fijo el dibujo por un rato, nos daremos cuenta que este ejercicio lo tenemos también prácticamente resuelto: basta trazar por
: Si miramos fijo el dibujo por un rato, nos daremos cuenta que este ejercicio lo tenemos también prácticamente resuelto: basta trazar por 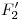 una perpendicular a
una perpendicular a  hasta cortarla. El segmento así determinado es la distancia
hasta cortarla. El segmento así determinado es la distancia 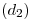 demandada.
demandada.
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported



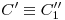 .
.