70.03 Medios de Representación "A" - Trabajo Práctico - Problemas de Magnitud

Período: 1er Cuatrimestre 2007

Alumno: García Mendive, Iñaki

Datos:

1. Hallar el ángulo 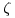entre y plano 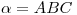: Para resolver este ejercicio, ángulo entre recta y plano, vamos a proceder de la siguiente forma: trazamos una normal al plano que corte a la recta dada, encontramos el ángulo que forman ambas, y 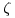resulta de restarle a 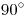. Antes de empezar, notemos que es proyectante sobre el ortográfico, ¿cómo lo sabemos? Bueno, porque notamos que contiene a una recta perpendicular al ortográfico (recta de punta), la 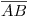. Esto nos resulta útil a la hora de trazar : 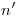debe ser perpendicular a 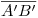al ser 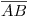una horizontal del plano. 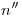debe ser perpendicular a , al ser éstas dos también coincidentes con la traza (si la dibujáramos) de . Ahora, ¿por dónde trazamos ? Bueno, la idea sería hacerlo por un punto más o menos cómodo de : el 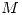, por ejemplo. 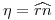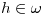Ahora resta encontrar , para lo cual haremos un rebatimiento del plano que forman ambas rectas sobre otro plano horizontal , alrededor de un eje ¹⁾. Los correspondientes puntos en icnografía 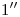de y de 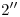determinan , el cual será a los fines prácticos el eje de abatimiento. 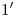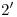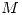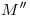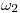Como y permanecen inmóviles durante esta operación, vemos que sólo necesitamos rebatir : por , perpendicular al eje, trasladamos la diferencia de elevaciones entre y (tenemos así 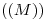). Luego trazamos por una perpendicular a : la intersección de ambas nos da 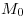(no nominado en el dibujo). Con centro en éste y extremo en 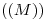trazamos un arco de circunferencia en sentido antihorario hasta cortar a 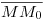: encontramos finalmente 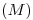. Lo unimos 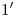con y con 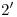para hallar respectivamente 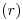y 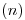, y entre ellas el ángulo . Como broche de gala, trazamos por 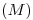una perpendicular a 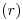: entre ella y 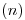tenemos a 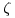. Aclaración: cuando se pide el ángulo entre recta y plano, por lo general es al agudo al que se hace referencia.
2. Hallar la distancia 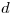entre el tanque y la cañería: en este ejercicio haremos uso del cambio de planos de proyección: el objetivo es llevar a 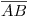(en icnografía o en ortografía) a la posición de recta de punta. En este caso particular, y por la posición de los datos (las dos proyecciones originales) en la hoja de dibujo, la llevaremos a una posición perpendicular al icnográfico. Para ello, primero desplazaremos a 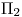de manera de tener a 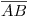en posición frental: para que esto ocurra, la nueva fundamental debe ser paralela a la icnografía 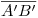que ya tenemos. ¡No caiga preso/a del desconcierto lector/a! Si no encuentra a 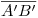, es porque no sólo hemos dibujado la fundamental paralela a ella, sino que, en un afán de dibujar menos líneas, las hemos hecho coincidir. Ahora, volviendo al tema que nos compete, ¿cómo encontramos 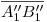? 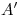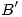Pues bien, es cuestión de trasladar las elevaciones originales de y , a partir de y sobre perpendiculares a y a . A 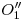, lo encontramos de manera similar, trasladando la distancia entre 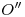y la fundamental original, sobre una perpendicular a trazada por , a partir de .
   Fabuloso, ahora que tenemos la recta en posición frental, podemos cambiar la posición de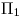 para obtenerla como recta de punta. Para ello, la nueva fundamental deberá ser perpendicular a 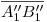. Para encontrar la nueva icnografía de 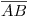debemos trasladar, sobre la prolongación de 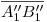y a partir de , la distancia de 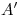a ²⁾, que es en este caso nula pues habíamos hecho coincidir a con 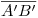. Resulta entonces . 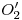Queda encontrar la nueva icnografía de 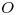. Para ello, llevamos, sobre una perpendicular a y a partir de ésta, la distancia de a . Por ser esférico el tanque, los sucesivos nuevos contornos aparentes de la misma (el del primer cambio de planos, y el del segundo también), son circunferencias idénticas a las originales. Trazamos entonces por 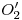una tal, y también un radio de la misma que, prolongado, contenga a . El segmento de radio comprendido entre ese punto y la circunferencia es la distancia 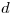pedida.