Tabla de Contenidos
70.03 Medios de Representación "A" - Trabajo Práctico - Intersecciones
Período: 1er Cuatrimestre 2007
Alumno: García Mendive, Iñaki
Lámina
Resolución
- Hallar la recta
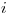 de intersección entre
de intersección entre  y
y 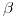 : Para encontrar un primer punto
: Para encontrar un primer punto  de
de 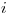 , empecemos por usar un plano
, empecemos por usar un plano 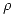 proyectante sobre el ortográfico. El mismo corta a
proyectante sobre el ortográfico. El mismo corta a 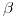 según
según 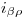 , definida por
, definida por  y
y  ; y a
; y a  según
según 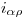 , definida por
, definida por  y
y 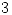 .
. 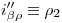 ,1) por lo cual fácilmente determinamos
,1) por lo cual fácilmente determinamos 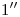 y, bajando por éste una vertical hasta
y, bajando por éste una vertical hasta 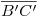 , tenemos
, tenemos 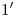 . Por
. Por 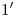 y
y 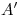 trazamos, con suma facilidad,
trazamos, con suma facilidad, 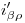 . En el caso de
. En el caso de  , también se da que
, también se da que 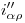 2), con lo cual ubicamos fácilmente a
2), con lo cual ubicamos fácilmente a 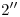 y a
y a 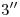 y, bajando por cada uno una vertical hasta
y, bajando por cada uno una vertical hasta 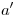 y
y 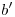 respectivamente, encontramos
respectivamente, encontramos 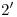 y
y 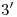 , por los cuales trazamos
, por los cuales trazamos  .
. 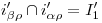 , y subiendo por éste una vertical hasta cortar a
, y subiendo por éste una vertical hasta cortar a 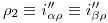 encontramos
encontramos 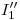 .
.
Para encontrar otro punto, de
de 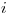 empleamos un plano
empleamos un plano 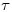 , el cual — en un arrebato de fiaca total — no sólo hemos elegido proyectante (sobre el icnográfico), sino que además hemos hecho coincidir su traza
, el cual — en un arrebato de fiaca total — no sólo hemos elegido proyectante (sobre el icnográfico), sino que además hemos hecho coincidir su traza 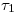 con
con 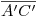 . Como consecuencia de esto,
. Como consecuencia de esto, 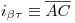 ,3) y sólo nos resta encontrar entonces
,3) y sólo nos resta encontrar entonces 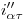 (recordar que
(recordar que  ). Subiendo una vertical por
). Subiendo una vertical por 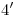 y por
y por 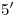 se encuentran respectivamente
se encuentran respectivamente 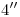 y
y 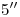 sobre
sobre 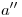 y
y 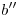 . Por estos dos se traza
. Por estos dos se traza 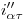 .
. 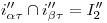 , así que bajando por éste una vertical hasta
, así que bajando por éste una vertical hasta 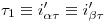 encontramos
encontramos 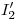 .
.
Uniendo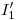 con
con 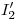 tenemos
tenemos 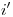 y uniendo
y uniendo 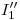 con
con 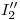 tenemos
tenemos 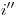 .
. - Hallar el punto
 de intersección entre
de intersección entre 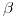 y
y  : Para esto utilizaremos un plano proyectante, que por arte de birlibirloque lo elegiremos sobre el ortográfico, siendo entonces
: Para esto utilizaremos un plano proyectante, que por arte de birlibirloque lo elegiremos sobre el ortográfico, siendo entonces 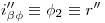 .
.  debe proyectar a
debe proyectar a  4) porque el método de resolución que empleamos en este caso es: encontrar la recta intersección entre ambos planos, y luego el punto que es intersección entre las dos rectas en cuestión. Para empezar,
4) porque el método de resolución que empleamos en este caso es: encontrar la recta intersección entre ambos planos, y luego el punto que es intersección entre las dos rectas en cuestión. Para empezar, 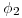 corta a
corta a 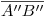 en
en 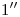 y a
y a 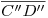 en
en 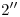 . Bajando estos puntos respectivamente a
. Bajando estos puntos respectivamente a 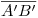 y a
y a 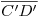 tenemos
tenemos 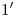 y
y 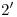 , por los cuales trazamos
, por los cuales trazamos 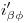 . La intersección de ésta con
. La intersección de ésta con 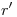 da
da 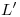 , y subiendo por éste una vertical hasta
, y subiendo por éste una vertical hasta 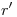 se trova
se trova 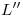 , con lo cual queda solucionado el problema.
, con lo cual queda solucionado el problema.
Queda evaluar la visibilidad: para ello empleamos el método de los puntos dobles, como ya hemos hecho aquí (una lámina dedicada casi completamente al tema de la visibilidad de las proyecciones). Puntos tales como el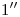 y el
y el 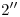 , en los cuales se cortan las ortografías
, en los cuales se cortan las ortografías 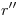 y
y 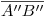 ó respectivamente
ó respectivamente 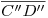 . Si, bajando una vertical por
. Si, bajando una vertical por 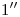 , miramos la icnografía notamos que el alejamiento de
, miramos la icnografía notamos que el alejamiento de 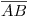 es mayor que el de
es mayor que el de  , (y lógicamente, si bajamos una vertical por
, (y lógicamente, si bajamos una vertical por 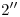 y miramos la icnografía, vemos que sucede lo contrario): podemos así determinar la visibilidad en ortografía. Para hacer lo propio en la primera proyección, debemos elegir otro par de puntos dobles: aquellos en donde se cortan las icnografías
y miramos la icnografía, vemos que sucede lo contrario): podemos así determinar la visibilidad en ortografía. Para hacer lo propio en la primera proyección, debemos elegir otro par de puntos dobles: aquellos en donde se cortan las icnografías 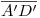 y
y 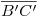 con
con 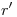 .
.
Nótese que, en este ejercicio, para estar seguros que los cuatro puntos dados sean coplanares, deben ser paralelas entre sí por lo menos dos de las cuatro rectas dadas. Caso contrario, habría que verificar si ellas forman realmente un plano. - Hallar la recta
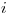 de intersección entre
de intersección entre  y
y 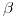 : Por la similitud entre éste ejercicio y el primero (y no sólo de nombre), omito la explicación de la resolución del mismo. Advierto, sin embargo, un error en la nomenclatura: donde dice
: Por la similitud entre éste ejercicio y el primero (y no sólo de nombre), omito la explicación de la resolución del mismo. Advierto, sin embargo, un error en la nomenclatura: donde dice  debería rezar
debería rezar 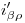 .
.
En lo que a visibilidad concierne, dada la similitud (quizás no tan aparente en primera instancia) con el ejercicio anterior, nos limitaremos a exponer el caso de la ortografía. Elegimos el punto doble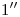 : bajando por él una vertical hasta cortar a
: bajando por él una vertical hasta cortar a 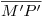 y a
y a 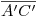 . La idea es determinar si, para ése punto,
. La idea es determinar si, para ése punto, 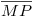 se encuentra delante de
se encuentra delante de 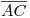 o viceversa. Como se observa en icnografía, es la segunda opción: dibujamos entonces
o viceversa. Como se observa en icnografía, es la segunda opción: dibujamos entonces 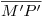 en trazo discontinuo desde
en trazo discontinuo desde 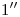 hasta
hasta 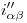 , y en consecuencia en trazo continuo de
, y en consecuencia en trazo continuo de 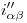 en adelante. Lógicamente (trate de visualizar la ortografía de los planos y cómo se intersecan),
en adelante. Lógicamente (trate de visualizar la ortografía de los planos y cómo se intersecan), 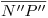 también debe dibujarse en trazo discontinuo entre
también debe dibujarse en trazo discontinuo entre 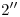 y
y 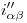 (por supuesto que esto se puede comprobar efectuando un procedimiento análogo al recién aplicado para el caso de
(por supuesto que esto se puede comprobar efectuando un procedimiento análogo al recién aplicado para el caso de 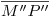 ). Observamos también que por todo esto
). Observamos también que por todo esto 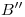 debe ser invisible y así también los segmentos involucrados de
debe ser invisible y así también los segmentos involucrados de 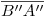 y
y 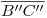 . Cabe aclarar: el estar ciertos segmentos de las proyecciones de
. Cabe aclarar: el estar ciertos segmentos de las proyecciones de 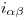 dibujados en línea de trazos no responde a temas de visibilidad.
dibujados en línea de trazos no responde a temas de visibilidad.
Sobre temas de intersección de planos, ver el Apéndice al primer tomo del libro Geometría Descriptiva del Ingeniero Eduardo Oscar di Lorenzo.
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported



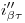 : en vez de ello, está escrito
: en vez de ello, está escrito 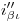 .
.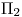 .
.