Tabla de Contenidos
70.03 Medios de Representación "A" - Trabajo Práctico - Problemas de Posición
Período: 1er Cuatrimestre 2007
Alumno: García Mendive, Iñaki
Lámina
Resolución:
- Hallar la tercera proyección de
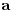 y
y  : Para ello vamos a tomar un par de puntos de cada recta. Como vemos, donde
: Para ello vamos a tomar un par de puntos de cada recta. Como vemos, donde 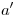 corta a
corta a 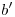 encontramos un punto doble, o sea, la icnografía coincidente de dos puntos (uno perteneciente a
encontramos un punto doble, o sea, la icnografía coincidente de dos puntos (uno perteneciente a  y el otro a
y el otro a  ). Ello también ocurre en el caso de
). Ello también ocurre en el caso de 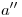 y de
y de 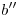 . Empecemos por la planta: nominamos al punto intersección de
. Empecemos por la planta: nominamos al punto intersección de 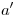 con
con 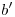 :
:  , y subamos una vertical por allí: donde corte a
, y subamos una vertical por allí: donde corte a 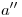 tendremos
tendremos 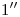 , y donde corte a
, y donde corte a 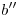 tendremos
tendremos 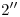 . Hemos encontrado así un punto (sus dos proyecciones) para cada recta. Ahora sigamos con la elevación: al punto que es
. Hemos encontrado así un punto (sus dos proyecciones) para cada recta. Ahora sigamos con la elevación: al punto que es 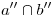 llamémoslo
llamémoslo  , y bajemos una vertical por él para trovar
, y bajemos una vertical por él para trovar 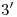 en
en 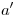 y
y 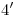 en
en 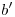 . Si podemos hallar la tercera proyección de estos cuatro puntos, habremos resuelto esta primera parte del ejercicio. Como sabemos, sus terceras proyecciones tienen igual elevación que sus ortografías: trazamos entonces por
. Si podemos hallar la tercera proyección de estos cuatro puntos, habremos resuelto esta primera parte del ejercicio. Como sabemos, sus terceras proyecciones tienen igual elevación que sus ortografías: trazamos entonces por 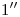 ,
, 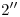 ,
, 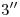 y
y 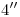 horizontales hasta más allá de la perpendicular a la fundamental (que es la traza ortográfica de
horizontales hasta más allá de la perpendicular a la fundamental (que es la traza ortográfica de 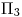 ). Sabemos también que las terceras proyecciones de los antedichos cuatro puntos tienen igual alejamiento que sus icnografías: trazamos entonces, por cada una de ellas, horizontales hasta cortar a la perpendicular a la fundamental (la traza icnográfica de
). Sabemos también que las terceras proyecciones de los antedichos cuatro puntos tienen igual alejamiento que sus icnografías: trazamos entonces, por cada una de ellas, horizontales hasta cortar a la perpendicular a la fundamental (la traza icnográfica de 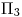 ). Allí, haciendo centro en la intersección de la traza icnográfica de
). Allí, haciendo centro en la intersección de la traza icnográfica de 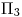 con la fundamental, y tomando como radios los alejamientos de los puntos en cuestión,1) trazamos arcos (de un cuarto de circunferencia de longitud) en sentido antihorario hasta cortar a la fundamental: por esos cuatro puntos levantamos verticales. Donde éstas corten a las correspondientes horizontales (trazadas por
con la fundamental, y tomando como radios los alejamientos de los puntos en cuestión,1) trazamos arcos (de un cuarto de circunferencia de longitud) en sentido antihorario hasta cortar a la fundamental: por esos cuatro puntos levantamos verticales. Donde éstas corten a las correspondientes horizontales (trazadas por 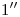 ,
, 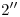 ,
, 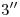 y
y 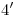 ) tendremos
) tendremos  ,
, 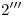 ,
,  y
y 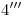 . Ahora sólo es cuestión de unir esos dos primeros entre sí (para obtener
. Ahora sólo es cuestión de unir esos dos primeros entre sí (para obtener  ) y estos dos últimos entre sí (para obtener
) y estos dos últimos entre sí (para obtener  ).
). - Hallar la visibilidad en cada una de las proyecciones: para esto usaremos el método de los puntos dobles: en efecto, no es casualidad que sean tales los puntos que hemos utilizado para el ejercicio anterior. Antes de empezar, encontremos otro par de puntos dobles: el de la tercera proyección. Así, tenemos
 . Para hallar
. Para hallar 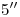 trazamos por
trazamos por 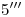 una horizontal hasta cortar a
una horizontal hasta cortar a 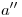 . Para hallar
. Para hallar 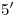 trazamos una vertical por
trazamos una vertical por 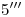 hasta cortar a la fundamental, por allí giramos en sentido horario hasta cortar a la traza icnográfica de
hasta cortar a la fundamental, por allí giramos en sentido horario hasta cortar a la traza icnográfica de 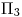 , y por allí trazamos una horizontal hasta cortar a
, y por allí trazamos una horizontal hasta cortar a 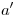 2). Lo mismo vale para
2). Lo mismo vale para 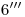 y
y  . Ahora sí, centrémonos en la visiblidad: primero, en icnografía. En este caso, lo que hay que determinar es cuál recta está arriba de (tiene mayor elevación que) otra y, en definitiva, se reduce a comparar las elevaciones de los puntos
. Ahora sí, centrémonos en la visiblidad: primero, en icnografía. En este caso, lo que hay que determinar es cuál recta está arriba de (tiene mayor elevación que) otra y, en definitiva, se reduce a comparar las elevaciones de los puntos  y
y  . Para ello, observemos la ortografía: claramente, el punto
. Para ello, observemos la ortografía: claramente, el punto  tiene mayor elevación que el punto
tiene mayor elevación que el punto  , es decir, si suponemos que vemos a los elementos en icnografía desde
, es decir, si suponemos que vemos a los elementos en icnografía desde 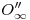 , notaríamos que
, notaríamos que  está por encima de
está por encima de  en el punto doble considerado (
en el punto doble considerado ( ). Para la visibilidad de la proyección ortográfica, nos fijamos en la icnografía: aquí el objetivo es comparar los alejamientos de
). Para la visibilidad de la proyección ortográfica, nos fijamos en la icnografía: aquí el objetivo es comparar los alejamientos de  y de
y de  en el punto doble
en el punto doble  . En planta se observa claramente que el alejamiento de
. En planta se observa claramente que el alejamiento de  es mayor que el de
es mayor que el de  , es decir que si miráramos a los cuerpos desde
, es decir que si miráramos a los cuerpos desde 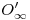 , veríamos a
, veríamos a  por delante de
por delante de  . Ahora centrémonos en la visibilidad de la tercera proyección: para ello podemos recurrir tanto a la icnografía como a la ortografía. Por comodidad, haremos uso de la segunda, y considerando el punto doble
. Ahora centrémonos en la visibilidad de la tercera proyección: para ello podemos recurrir tanto a la icnografía como a la ortografía. Por comodidad, haremos uso de la segunda, y considerando el punto doble  . Vemos entonces que el punto
. Vemos entonces que el punto  está a una mayor distancia de
está a una mayor distancia de 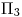 que el
que el 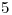 , es decir que, si observáramos los caños desde un punto a la izquierda 3) infinitamente alejado del plano de tercera proyección, veríamos la recta
, es decir que, si observáramos los caños desde un punto a la izquierda 3) infinitamente alejado del plano de tercera proyección, veríamos la recta  por delante de la
por delante de la  . Una vez trazados los segmentos pertinentes, quedan completas las tres proyecciones de los cuerpos, y con ellas, la lámina.
. Una vez trazados los segmentos pertinentes, quedan completas las tres proyecciones de los cuerpos, y con ellas, la lámina.
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported


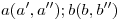 : ejes de dos conductos (⌀
: ejes de dos conductos (⌀ ) que se cruzan.
) que se cruzan.
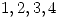 .
.