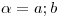70.03 Medios de Representación "A" - Trabajo Práctico - Problemas de Posición

Período: 1er Cuatrimestre 2007

Alumno: García Mendive, Iñaki

Datos:

1. pertenece a
   
   
2. Plano
   

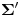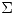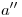1. Hallar : Si pertenece a , entonces las tres rectas que la delimitan deben también pertenecer a . Hallemos pues la icnografía de , de y de , para lo cual nos valdremos de las proyecciones de ciertos puntos notables suyos: sus trazas. Así, por ejemplo, para : donde corta a 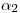tenemos 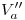, y donde 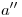corta a la fundamental tenemos 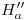. Si por 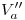bajamos una vertical hasta la línea de tierra, tenemos 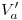, y si por 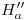bajamos una vertical hasta 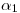tenemos 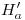: éstos dos son puntos de la icnografía 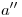que buscábamos. 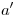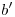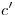De idéntica manera procedemos para y para : el área delimitada por , y es 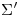. Cabe subrayar que este ejercicio es muy similar al primer ejercicio de este parcialito.
2. Hallar las trazas 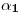y 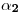: Primero, cerciorémonos de que y sean coplanares: vemos que 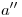y 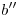se cortan en un punto que llamaremos 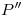. Si ahora bajamos una vertical por 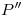hasta 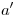, allí debemos encontrar también a 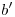: es decir, debemos hallar a 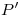. De otra forma, y no formarían un plano. Lo forman, sin embargo, como podemos claramente observar. Nos dedicamos entonces, ahora sí, a encontrar aquellas trazas que nos piden. Para empezar, debemos tener en claro ciertos aspectos fundamentales: 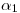pasa 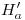por y por 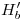, al ser estos respectivamente 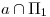y 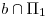(id est, las trazas de y de ). 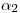Análogamente, contiene 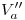a y a 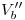. Ahora bien, ¿cómo encontramos estos cuatro puntos? Para 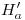: donde 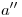corta a la fundamental, tenemos 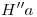(punto de elevación nula de ), y bajando por éste una vertical hasta 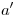hallamos 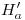. Para 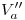: donde 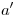corta a la línea de tierra encontramos 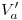(punto de alejamiento nulo de ), y subiendo por éste una vertical hasta 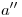trovamos 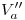. Lo mismo se aplica para . 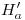Uniendo con 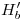obtenemos 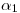, y uniendo 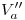con 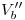obtenemos 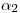. Si no ha habido errores groseros en el trazado, 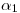, 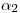y la fundamental deberían cortarse en un mismo punto.